题目内容
圆C的极坐标方程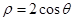 化为直角坐标方程为 ,该圆的面积为 .
化为直角坐标方程为 ,该圆的面积为 .
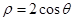 化为直角坐标方程为 ,该圆的面积为 .
化为直角坐标方程为 ,该圆的面积为 .x2+y2-2x=0 π
此题答案应为:x2+y2-2x=0 π
先在极坐标方程p=2cosθ的两边同乘以ρ,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.
解:将方程p=2cosθ两边都乘以p得:p2=2pcosθ,
化成直角坐标方程为
x2+y2-2x=0.半径为1,面积为π.
故填:x2+y2-2x=0 π.
先在极坐标方程p=2cosθ的两边同乘以ρ,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.
解:将方程p=2cosθ两边都乘以p得:p2=2pcosθ,
化成直角坐标方程为
x2+y2-2x=0.半径为1,面积为π.
故填:x2+y2-2x=0 π.

练习册系列答案
相关题目
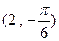 到直线:
到直线: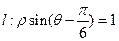 的距离是 .
的距离是 .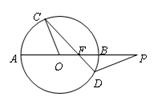
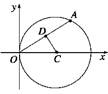
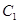 和
和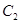 的方程分别为
的方程分别为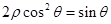 和
和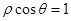 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为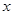 轴正半轴,建立平面直角坐标系,则曲线
轴正半轴,建立平面直角坐标系,则曲线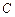 的极坐标方程是
的极坐标方程是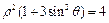 ,直线
,直线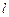 的参数方程是
的参数方程是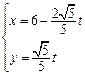
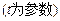 .
.
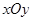 中,点P的直角坐标为
中,点P的直角坐标为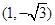 。若以原点O为极点,
。若以原点O为极点,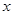 轴正半轴为极轴建立坐标系,则点P的极坐标可以是 ( )
轴正半轴为极轴建立坐标系,则点P的极坐标可以是 ( )
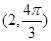


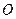 是极点,设点
是极点,设点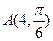 ,
,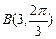 ,则O点到AB所在直线的距离是 .
,则O点到AB所在直线的距离是 .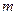 的方程为
的方程为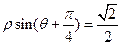 ,则点
,则点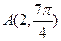 到直线
到直线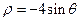 和
和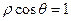 相交于点
相交于点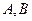 ,则
,则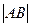 = .
= .