题目内容
 ,对
,对 使
使
 ,则
,则 的取值范围是
的取值范围是
A. | B. | C. | D. |
A
解析试题分析:根据题意,由于 ,对
,对 使
使
 ,则只要满足二次函数的函数的值域在
,则只要满足二次函数的函数的值域在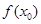 的范围内即可,结合二次函数性质可知
的范围内即可,结合二次函数性质可知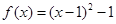 ,在
,在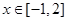 时值域为
时值域为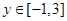
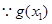 是递增的一次函数可知,
是递增的一次函数可知,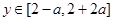 ,则可知
,则可知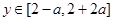 包含于集合
包含于集合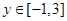 中可知,参数a的范围是
中可知,参数a的范围是 ,选A.
,选A.
考点:二次函数的性质
点评:解决的关键是理解全称命题和特称命题的关系,以及准确的运用,属于基础题。

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
函数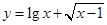 的定义域是( )
的定义域是( )
A.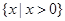 | B. | C.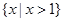 | D.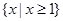 |
函数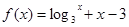 零点所在大致区间是( )
零点所在大致区间是( )
| A.(1,2) | B.(2,3) | C.(3,4) | D.(4,5) |
设 ,用二分法求方程
,用二分法求方程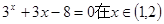 内近似解的过程
内近似解的过程
中得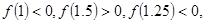 则方程的根落在区间
则方程的根落在区间
A.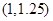 | B. | C.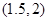 | D.不能确定 |
设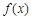 在
在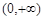 上是单调递增函数,当
上是单调递增函数,当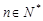 时,
时,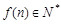 ,且
,且 ,则( )
,则( )
A.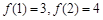 | B. |
C.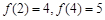  | D.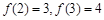 |
若函数 与函数
与函数 在区间
在区间 上都是减函数,则实数的取值范围为( )
上都是减函数,则实数的取值范围为( )
A. | B. | C. | D.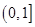 |
下列函数在区间[0, ]上是减函数的是
]上是减函数的是
| A.y="sin" x | B.y="cos" x | C.y="tan" x | D.y=2 |
函数 的单调递减区间是 ( )
的单调递减区间是 ( )
A. | B. | C. | D. |
设 ,用二分法求方程
,用二分法求方程 内近似解的过程中得
内近似解的过程中得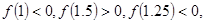 则方程的根落在区间( )
则方程的根落在区间( )
A. | B. | C. | D.不能确定 |