题目内容
已知点 分别是椭圆
分别是椭圆 的左、右焦点,过
的左、右焦点,过 且垂直于
且垂直于 轴的直线与椭圆交于A、B两点,若
轴的直线与椭圆交于A、B两点,若 为正三角形,则该椭圆的离心率
为正三角形,则该椭圆的离心率 是( )
是( )
A. | B. | C. | D. |
D
解析试题分析:因为 为正三角形,所以
为正三角形,所以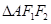 为直角三角形,在此三角形中,
为直角三角形,在此三角形中, ,再将
,再将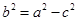 代入,可以求得该椭圆的离心率
代入,可以求得该椭圆的离心率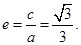
考点:本小题主要考查椭圆的性质,椭圆的离心率.
点评:椭圆中基本量之间的关系要准确掌握,灵活应用,离心率的求解是考查的重点.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
双曲线 =1的焦点到渐近线的距离为( )。
=1的焦点到渐近线的距离为( )。
A.2 | B.2 | C. | D.1 |
抛物线 上的点到直线
上的点到直线 距离的最小值是( )
距离的最小值是( )
A. | B. | C. | D. |
下列命题中真命题的是( )
| A.在同一平面内,动点到两定点的距离之差(大于两定点间的距离)为常数的点的轨迹是双曲线 |
| B.在平面内,F1,F2是定点,|F1F2|=6,动点M满足|MF1|+|MF2|=6,则点M的轨迹是椭圆 |
C.“若-3<m<5则方程 是椭圆” 是椭圆” |
D.在直角坐标平面内,到点 和直线 和直线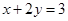 距离相等的点的轨迹是直线 距离相等的点的轨迹是直线 |
如果过曲线 上点
上点 处的切线平行于直线
处的切线平行于直线 ,那么点
,那么点 的坐标为
的坐标为
A. | B. | C. | D.( |
 ,
, 分别是双曲线
分别是双曲线 的左、右焦点,过点
的左、右焦点,过点 为直径的圆外,则双曲线离心率的取值范围是
为直径的圆外,则双曲线离心率的取值范围是



 ,虚轴的一个端点为
,虚轴的一个端点为 ,如果直线
,如果直线 与该双曲线的一条渐近线垂直,那么双曲线的离心率是 ( )
与该双曲线的一条渐近线垂直,那么双曲线的离心率是 ( )



 、
、 是椭圆
是椭圆 (a>b>0)的两个焦点,以线段
(a>b>0)的两个焦点,以线段


 上一个动点,Q为圆
上一个动点,Q为圆 上一个动点,那么点P到点Q的距离与点P到
上一个动点,那么点P到点Q的距离与点P到 轴距离之和最小值是( )
轴距离之和最小值是( )



