题目内容
已知二次函数f(x)的二次项系数a(a≠0),且不等式f(x)<2x的解集为(-1,2).
(1)若方程f(x)+3a=0有两个相等的实根,求f(x)的解析式;
(2)若函数f(x)的最小值不大于-3a,且函数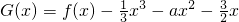 在R上为减函数,求实数a的取值范围.
在R上为减函数,求实数a的取值范围.
解:(1)设二次函数为f(x)=ax2+bx+c
∵f(x)<2x的解集为(-1,2).
∴-1,2是方程ax2+(b-2)x+c=0的两个根
∴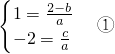
∵方程f(x)+3a=0有两个相等的实根即
ax2+bx+c+3a=0有两个相等的实根
∴△=b2-4a(c+3a)=0②
解①②得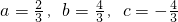
∴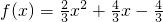
(2)根据题意得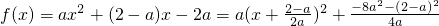
∵a>0,所以f(x)的最小值为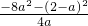
则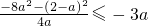
得
由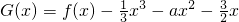 在R上是减函数,
在R上是减函数,
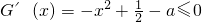 在R上恒成立
在R上恒成立
∴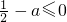
得到 ,
,
综上所述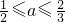
分析:(1)据二次不等式的解集与相应的二次方程的根的关系,判断出-1,2是方程的根,利用韦达定理列出a,b,c满足的等式;再利用二次方程有两个相等的实根,判别式等于0列出关于a,b,c的另一个等式,解方程组求出f(x)的解析式.
(2)通过对二次函数配方求出其最小值,列出不等式求出a的范围;求出G(x)的导函数,令其大于等于0恒成立,求出a的范围.
点评:解决二次不等式的解集问题常转化为二次方程的根问题,利用韦达定理得到系数间的关系;解决函数在某个区间上的单调性已知,求参数的范围问题,常求出函数的导函数,令导函数大于等于0(或小于等于0)恒成立.
∵f(x)<2x的解集为(-1,2).
∴-1,2是方程ax2+(b-2)x+c=0的两个根
∴
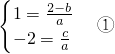
∵方程f(x)+3a=0有两个相等的实根即
ax2+bx+c+3a=0有两个相等的实根
∴△=b2-4a(c+3a)=0②
解①②得
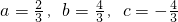
∴
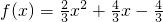
(2)根据题意得
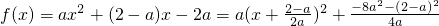
∵a>0,所以f(x)的最小值为
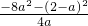
则
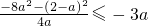
得

由
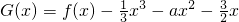 在R上是减函数,
在R上是减函数,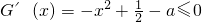 在R上恒成立
在R上恒成立∴
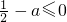
得到
 ,
,综上所述
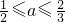
分析:(1)据二次不等式的解集与相应的二次方程的根的关系,判断出-1,2是方程的根,利用韦达定理列出a,b,c满足的等式;再利用二次方程有两个相等的实根,判别式等于0列出关于a,b,c的另一个等式,解方程组求出f(x)的解析式.
(2)通过对二次函数配方求出其最小值,列出不等式求出a的范围;求出G(x)的导函数,令其大于等于0恒成立,求出a的范围.
点评:解决二次不等式的解集问题常转化为二次方程的根问题,利用韦达定理得到系数间的关系;解决函数在某个区间上的单调性已知,求参数的范围问题,常求出函数的导函数,令导函数大于等于0(或小于等于0)恒成立.

练习册系列答案
相关题目