题目内容
16．求椭圆的离心率：（1）长轴长和短轴长分别为26和24；
（2）一焦点坐标为（5，0），短轴长为6．
分析 （1）由题意可得a=13，b=12，c=$\sqrt{{a}^{2}-{b}^{2}}$=5，运用离心率公式计算即可得到；
（2）由题意可得c=5，b=3，由a=$\sqrt{{b}^{2}+{c}^{2}}$求得a，再由离心率公式即可得到所求．
解答 解：（1）由题意可得2a=26，2b=24，
即有a=13，b=12，c=$\sqrt{{a}^{2}-{b}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5，
则离心率e=$\frac{c}{a}$=$\frac{5}{13}$；
（2）由题意可得c=5，2b=6，
即b=3，a=$\sqrt{{b}^{2}+{c}^{2}}$=$\sqrt{9+25}$=$\sqrt{34}$，
则离心率e=$\frac{c}{a}$=$\frac{5}{\sqrt{34}}$=$\frac{5\sqrt{34}}{34}$．
点评 本题考查椭圆的离心率的求法，注意运用椭圆的a，b，c的关系，求得a，c是解题的关键．
练习册系列答案
计算高手系列答案
相关题目
6．命题p：?x＞0，总有x2-1≥0，则?p为（ ）
| A． | ?x0≤0，使得x2-1＜0 | B． | ?x0＞0，使得x2-1＜0 | ||
| C． | ?x＞0，总有x2-1＜0 | D． | ?x≤0，总有x2-1＜0 |
1．
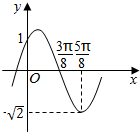函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ≤$\frac{π}{2}$）的图象如图所示，将f（x）的图象向左平移$\frac{π}{8}$个单位后得到函数g（x）的图象，则（ ）
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ≤$\frac{π}{2}$）的图象如图所示，将f（x）的图象向左平移$\frac{π}{8}$个单位后得到函数g（x）的图象，则（ ）| A． | g（x）=$\sqrt{2}$sin（2x+$\frac{3π}{8}$） | B． | g（x）=$\sqrt{2}$cos2x | C． | g（x）=$\sqrt{2}$cos（2x+$\frac{3π}{8}$） | D． | g（x）=$\sqrt{2}$sin2x |