题目内容
9.已知θ∈R,则t=$\frac{1}{si{n}^{2}θ}$+$\frac{1}{co{s}^{2}θ}$的最小值是4.分析 由三角函数公式化简可得t=$\frac{4}{si{n}^{2}2θ}$,易得当sin2θ=±1时,上式取最小值4
解答 解:化简可得t=$\frac{1}{si{n}^{2}θ}$+$\frac{1}{co{s}^{2}θ}$
=$\frac{co{s}^{2}θ+si{n}^{2}θ}{si{n}^{2}θco{s}^{2}θ}$
=$\frac{1}{(sinθcosθ)^{2}}$=$\frac{4}{si{n}^{2}2θ}$
当sin2θ=±1时,上式取最小值4
故答案为:小;4
点评 本题考查三角函数的最值,涉及二倍角的正弦公式,属基础题.

练习册系列答案
相关题目
20.方程y2=x表示同一条曲线的参数方程(t为参数)的是( )
| A. | $\left\{\begin{array}{l}{x=si{n}^{2}t}\\{y=sint}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=t}\\{y={t}^{2}}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x=\frac{1-cos2t}{1+cos2t}}\\{y=tant}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=t}\\{y=\sqrt{|t|}}\end{array}\right.$ |
14.数列{an}中,an=n2-9n-100,则最小的项是( )
| A. | 第4项 | B. | 第5项 | C. | 第6项 | D. | 第4项或第5项 |
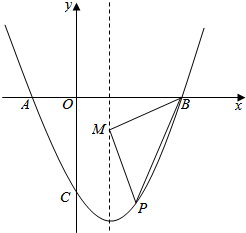 如图,抛物线y=(x-1)2+n与x轴交于A、B两点,A在B的左侧,与y轴交于C(0,-3).
如图,抛物线y=(x-1)2+n与x轴交于A、B两点,A在B的左侧,与y轴交于C(0,-3).