题目内容

16．方程cosx=lgx的实根的个数是（　　）
A．1B．2C．3D．无数

分析 本题即求函数y=cosx的图象和 y=lgx的图象的交点个数，数形结合可得结论．

解答 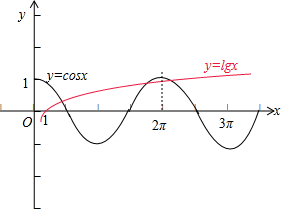解：方程cosx=lgx的实根的个数，即函数y=cosx的图象和 y=lgx的图象的交点个数，
数形结合可得函数y=cosx的图象和 y=lgx的图象的交点个数为3，
故选：C．

点评 本题主要考查方程根的存在性以及个数判断，余弦函数、对数函数的图象特征，体现了转化、数形结合的数学思想，属于基础题．

练习册系列答案
相关题目
6．已知定义在R上的函数y=f（x）的导函数为f′（x），满足f′（x）＜f（x），且f（0）=1，则不等式f（x）＜ex的解集为（　　）
A．（-∞，e4）B．（e4，+∞）C．（-∞，0）D．（0，+∞）
7．双曲线$\frac{x^2}{16}-\frac{y^2}{4}=1$的离心率e的值为（　　）
A．$\frac{{\sqrt{5}}}{2}$B．$\frac{{\sqrt{6}}}{2}$C．$\sqrt{2}$D．2
4．已知：$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$是同一平面内的三个向量，其中向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-3，2）
（1）若k$\overrightarrow{a}$+2$\overrightarrow{b}$与2$\overrightarrow{a}$-4$\overrightarrow{b}$平行，求实数k的值；
（2）若k$\overrightarrow{a}$+2$\overrightarrow{b}$与2$\overrightarrow{a}$-4$\overrightarrow{b}$垂直，求实数k的值．
（3）若|$\overrightarrow{c}$|=2$\sqrt{5}$，且$\overrightarrow{c}$∥$\overrightarrow{a}$，求$\overrightarrow{c}$的坐标．
11．定义在（-∞，+∞）上的偶函数f（x）满足f（x+1）=-f（x），且在[-1，0]上是增函数，下面是关于f（x）的判断：
①f（8）=f（0）
②f（x）在[0，1]上是增函数；
③f（x）的图象关于直线x=1对称
④f（x）关于点P（$\frac{1}{2}，0$）对称．
其中正确的判断是①③④．
1．下列函数为奇函数的是（　　）
A．y=|sin x|B．y=|x|C．y=x3+x-1D．y=ln $\frac{1+x}{1-x}$
8．若函数为f（x）=x2-2mx-2m-1
（1）求f（x）＞0的解集；
（2）若f（x）＞-4m-2对满足0≤x≤1的所有实数x都成立，求m的取值范围．
5．已知Sn=2n2+4n，设{$\frac{1}{{S}_{n}}$}的前n项和为Tn，证明：$\frac{1}{6}$≤Tn≤$\frac{3}{8}$．
6．已知向量$\overrightarrow a，\overrightarrow b$满足：$|{\overrightarrow a}|=1，|{\overrightarrow b}|=2$，$\overrightarrow a$与$\overrightarrow b$的夹角为$\frac{π}{3}$，则$|{2\overrightarrow a-\overrightarrow b}|$=（　　）
A．2B．4C．2$\sqrt{2}$D．8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网