题目内容
已知函数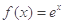

(1)求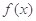 在点
在点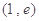 处的切线方程;
处的切线方程;
(2)证明:曲线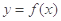 与曲线
与曲线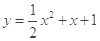 有唯一公共点;
有唯一公共点;
(3)设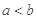 ,比较
,比较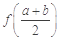 与
与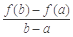 的大小, 并说明理由.
的大小, 并说明理由.
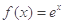

(1)求
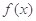 在点
在点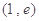 处的切线方程;
处的切线方程; (2)证明:曲线
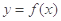 与曲线
与曲线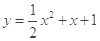 有唯一公共点;
有唯一公共点; (3)设
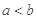 ,比较
,比较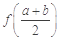 与
与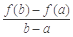 的大小, 并说明理由.
的大小, 并说明理由.(1)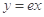
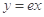
试题分析:(1)首先求出
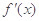 ,令
,令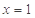 ,即可求出
,即可求出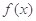 在点
在点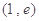 处的切线方程的斜率,代入点斜式即可求出切线方程
处的切线方程的斜率,代入点斜式即可求出切线方程(2)令
 则
则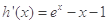 ,根据
,根据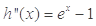 ,讨论
,讨论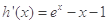 在
在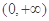 上单调递增,所以
上单调递增,所以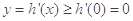 ,所以
,所以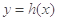 在
在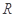 上单调递增,
上单调递增,,又
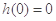 ,即函数
,即函数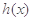 有唯一零点
有唯一零点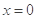 ,所以曲线
,所以曲线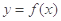 与曲线
与曲线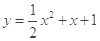 有唯一公共点
有唯一公共点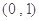 .
.(3)作差得
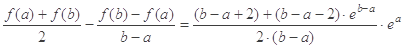 ,令
,令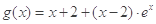 ,讨论
,讨论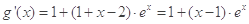 ,
,  的单调性,得到
的单调性,得到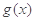 在
在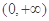 上单调递增,而
上单调递增,而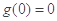 ,所以在
,所以在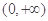 上
上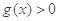 ,可得
,可得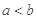 时,
时,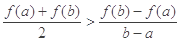
(1)
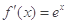 ,则
,则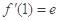 ,
,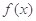 点
点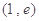 处的切线方程为:
处的切线方程为: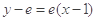 ,
,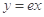
(2) 令
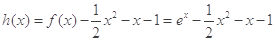 ,
, ,则
,则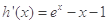 ,
,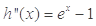
且
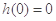 ,
,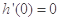 ,
,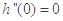
因此,当
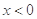 时,
时,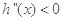 ,
,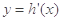 单调递减;当
单调递减;当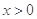 时,
时,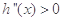 ,
,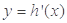 单调递增.
单调递增.所以
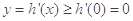 ,所以
,所以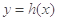 在
在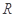 上单调递增,又
上单调递增,又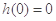 ,即函数
,即函数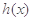 有唯一零点
有唯一零点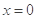 ,
,所以曲线
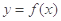 与曲线
与曲线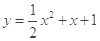 有唯一公共点
有唯一公共点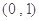 .
.(3) 设

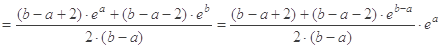
令
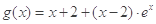 且
且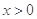 ,则
,则 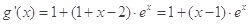
 ,所以
,所以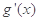 在
在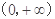 上单调增,且
上单调增,且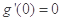 ,
,因此
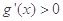 ,
,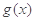 在
在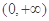 上单调递增,而
上单调递增,而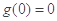 ,所以在
,所以在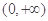 上
上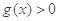
即当
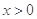 时,
时,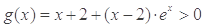 且
且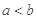 ,
,所以
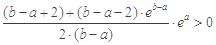 ,
,所以当
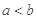 时,
时,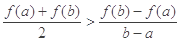

练习册系列答案
相关题目
 ,函数
,函数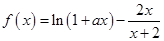 .
.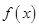 在区间
在区间 上的单调性;
上的单调性;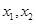 ,且
,且 ,求
,求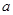 的取值范围.
的取值范围.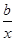 ,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.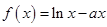 .
.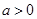 时,求函数
时,求函数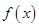 在区间
在区间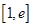 内的最大值;
内的最大值;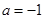 时,方程
时,方程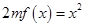 有唯一实数解,求正数
有唯一实数解,求正数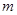 的值.
的值. 在
在 及
及 处取得极值.
处取得极值. 、
、 的值;(2)求
的值;(2)求 的单调区间.
的单调区间.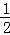 对称,且f′(1)=0
对称,且f′(1)=0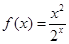 在区间
在区间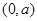 内单调,则
内单调,则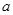 的最大值为__________.
的最大值为__________.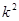 ,若
,若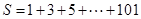 ( )
( )