题目内容
【题目】已知椭圆
的离心率为
，以椭圆的2个焦点与1个短轴端点为顶点的三角形的面积为2
。
（1）求椭圆的方程；
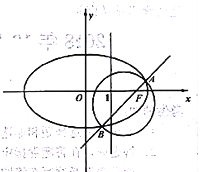
（2）如图，斜率为k的直线l过椭圆的右焦点F，且与椭圆交与A，B两点，以线段AB为直径的圆截直线x＝1所得的弦的长度为
，求直线l的方程。
【答案】（1）
；（2）
或
.
【解析】
（1）根据椭圆的离心率，三角形的面积建立方程，结合a2＝b2+c2，即可求椭圆C的方程；
（2）联立直线方程与椭圆联立，利用韦达定理表示出
及
，结合弦的长度为
，即可求斜率k的值，从而求得直线方程。
解：（1）由椭圆
的离心率为
，
得
，
.
由
得
， 
，所以椭圆方程为．
（2）解：设直线
，
，
，
中点
．
联立方程
得
，
.
．
所以
，
点
到直线
的距离为
．
由以线段为直径的圆截直线所得的弦的长度为得
，所以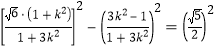
，
解得
，所以直线
的方程为
或
．
练习册系列答案
阅读快车系列答案
相关题目
