题目内容
已知函数 ,
, .
.
(Ⅰ)若 在
在 上为单调函数,求m的取值范围;
上为单调函数,求m的取值范围;
(Ⅱ)设 ,若在
,若在 上至少存在一个
上至少存在一个 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
(Ⅰ)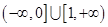 (Ⅱ)
(Ⅱ)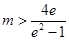
解析试题分析:(Ⅰ)f(x)-g(x)=mx-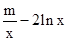 ,
,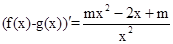
由于f(x)-g(x)在其定义域内为单调函数,则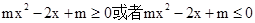 在
在 上恒成立,
上恒成立,
即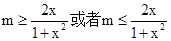 在
在 上恒成立,
上恒成立,
故 ,
,
综上,m的取值范围是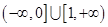 …6分
…6分
(Ⅱ)构造函数F(x)=f(x)-g(x)-h(x),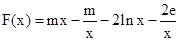 ,
,
当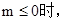 由
由 得,
得, ,
,
所以在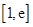 上不存在一个
上不存在一个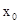 ,使得
,使得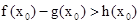 ; …………10分
; …………10分
当m>0时, ,
,
因为 ,所以
,所以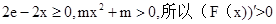 在
在 上恒成立,故F(x)在
上恒成立,故F(x)在 上单调递增,
上单调递增,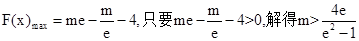 ,
,
故m的取值范围是 …………15分
…………15分
另法:(3) 令
令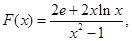
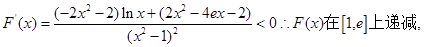
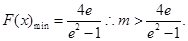
考点:利用函数导数判定单调性求函数最值
点评:若已知函数 在某区间上是增函数,则有
在某区间上是增函数,则有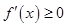 在该区间上恒成立;若已知函数
在该区间上恒成立;若已知函数 在某区间上是减函数,则有
在某区间上是减函数,则有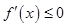 在该区间上恒成立。第二问首先将不等式成立转化为求函数最值,进而构造新函数,通过导数工具求其最值
在该区间上恒成立。第二问首先将不等式成立转化为求函数最值,进而构造新函数,通过导数工具求其最值

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 的定义域为
的定义域为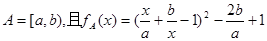 ,其中a、b为任
,其中a、b为任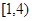 时,研究
时,研究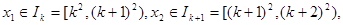 其中k是正整数,对一切正整数k不等式
其中k是正整数,对一切正整数k不等式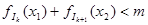 都有解,求m的取值范围。
都有解,求m的取值范围。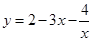 的值域.
的值域. ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 .
. 的解析式;
的解析式; 能作几条直线与曲线
能作几条直线与曲线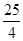 )ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.
)ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.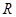 上的函数
上的函数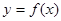 ,
,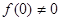 ,当
,当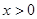 时,
时,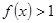 .且对任意的
.且对任意的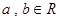 有
有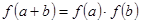 。
。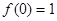 ;
;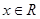 ,恒有
,恒有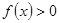 ;
;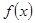 是
是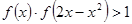 ,求
,求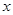 的取值范围。
的取值范围。 。
。 时,求函数
时,求函数 的最小值;
的最小值; 时,求实数
时,求实数 的取值范围。
的取值范围。 ,其图象在点
,其图象在点 处的切线方程为
处的切线方程为
 的值;
的值; 的单调区间,并求出
的单调区间,并求出