题目内容
 已知如图,圆C的圆心在抛物线x2=2py(p>0)上运动,且圆C过A(0,p)点,若MN为圆C在x轴上截得的弦.
已知如图,圆C的圆心在抛物线x2=2py(p>0)上运动,且圆C过A(0,p)点,若MN为圆C在x轴上截得的弦.
设AM=l1,AN=l2,求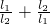 的取值范围.
的取值范围.
解:设∠MAN=θ,
因为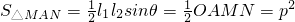 ,
,
所以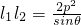 ,因为l12+l22-2l1l2cosθ=4p2,
,因为l12+l22-2l1l2cosθ=4p2,
所以l12+l22=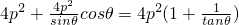 .
.
所以 .
.
因为0<θ≤900,所以当且仅当θ=45°时,原式有最大值 ,当且仅当θ=90°时,原式有最小值为2,从而
,当且仅当θ=90°时,原式有最小值为2,从而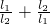 的取值范围为
的取值范围为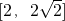 .
.
分析:设∠MAN=θ,由题意知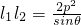 ,l12+l22=
,l12+l22=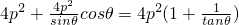 .所以
.所以 .由此可知当且仅当θ=45°时,原式有最大值
.由此可知当且仅当θ=45°时,原式有最大值 ,当且仅当θ=90°时,原式有最小值为2,从而
,当且仅当θ=90°时,原式有最小值为2,从而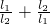 的取值范围.
的取值范围.
点评:本题考查圆锥曲线的位置关系和应用,解题时要认真审题和仔细解答.
因为
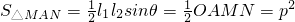 ,
,所以
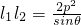 ,因为l12+l22-2l1l2cosθ=4p2,
,因为l12+l22-2l1l2cosθ=4p2,所以l12+l22=
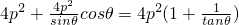 .
.所以
 .
.因为0<θ≤900,所以当且仅当θ=45°时,原式有最大值
 ,当且仅当θ=90°时,原式有最小值为2,从而
,当且仅当θ=90°时,原式有最小值为2,从而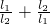 的取值范围为
的取值范围为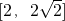 .
.分析:设∠MAN=θ,由题意知
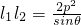 ,l12+l22=
,l12+l22=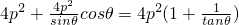 .所以
.所以 .由此可知当且仅当θ=45°时,原式有最大值
.由此可知当且仅当θ=45°时,原式有最大值 ,当且仅当θ=90°时,原式有最小值为2,从而
,当且仅当θ=90°时,原式有最小值为2,从而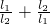 的取值范围.
的取值范围.点评:本题考查圆锥曲线的位置关系和应用,解题时要认真审题和仔细解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
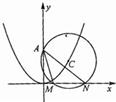 已知如图,圆C的圆心在抛物线x2=2py(p>0)上运动,且圆C过A(0,p)点,若MN为圆C在x轴上截得的弦.
已知如图,圆C的圆心在抛物线x2=2py(p>0)上运动,且圆C过A(0,p)点,若MN为圆C在x轴上截得的弦. 如图,已知圆C的圆心坐标为(1,-1),且过点M(2,-1).
如图,已知圆C的圆心坐标为(1,-1),且过点M(2,-1). [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.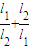 的取值范围.
的取值范围.