题目内容
 如图,已知圆C的圆心坐标为(1,-1),且过点M(2,-1).
如图,已知圆C的圆心坐标为(1,-1),且过点M(2,-1).(1)求圆C的标准方程;
(2)过点N(-1,-2)且斜率为1的直线l与圆C相交于A、B两点,求线段AB的长.
分析:(1)根据题意,设圆C的方程为(x-1)2+(y+1)2=r2,将点M(2,-1)的坐标代入算出r的值,即可得出圆C的标准方程;
(2)求出直线l方程为x-y-1=0,利用点到直线的距离公式算出点C到直线l的距离,再利用垂径定理加以计算,即可得到直线l被圆C截得的线段AB长.
(2)求出直线l方程为x-y-1=0,利用点到直线的距离公式算出点C到直线l的距离,再利用垂径定理加以计算,即可得到直线l被圆C截得的线段AB长.
解答:解:(1)∵圆C的圆心坐标为(1,-1),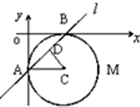
∴设圆C的方程为(x-1)2+(y+1)2=r2.
∵点M(2,-1)在圆C上,
∴(2-1)2+(-1+1)2=r2,解之得r=1(舍负).
∴圆C的标准方程为(x-1)2+(y+1)2=1;
(2)∵直线l过点N(-1,-2)且斜率为1,
∴直线l方程为y+2=x+1,即x-y-1=0
过C作CD⊥AB于点D,连结AC,则D为AB的中点
Rt△ACD中,AD=
∵CD=
=
∴AB=2AD=2
=

∴设圆C的方程为(x-1)2+(y+1)2=r2.
∵点M(2,-1)在圆C上,
∴(2-1)2+(-1+1)2=r2,解之得r=1(舍负).
∴圆C的标准方程为(x-1)2+(y+1)2=1;
(2)∵直线l过点N(-1,-2)且斜率为1,
∴直线l方程为y+2=x+1,即x-y-1=0
过C作CD⊥AB于点D,连结AC,则D为AB的中点
Rt△ACD中,AD=
| CA2-CD2 |
∵CD=
| |1+1-1| | ||
|
| ||
| 2 |
∴AB=2AD=2
| CA2-CD2 |
| 2 |
点评:本题给出圆满足的条件,求圆的方程并求定直线被圆截得的弦长.着重考查了直线的方程、圆的方程和直线与圆的位置关系等知识,属于中档题.

练习册系列答案
相关题目
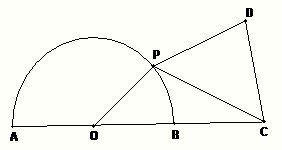 如图:已知圆O的直径是2,点C在直径AB的延长线上,BC=1,点P是圆O上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC的两侧,求四边形OPDC面积的最大值.
如图:已知圆O的直径是2,点C在直径AB的延长线上,BC=1,点P是圆O上的一个动点,以PC为边作正三角形PCD,且点D与圆心分别在PC的两侧,求四边形OPDC面积的最大值.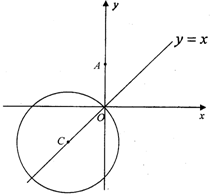 如图,已知圆C:x2+y2+10x+10y=0,点A(0,6).
如图,已知圆C:x2+y2+10x+10y=0,点A(0,6). (考生注意:请在二题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在二题中任选一题作答,如果多做,则按所做的第一题评分) (2012•黄冈模拟)(选做题:请在下列两题中任选一题作答,如果多做,则按所做的第一题评分)
(2012•黄冈模拟)(选做题:请在下列两题中任选一题作答,如果多做,则按所做的第一题评分)