题目内容
已知A、B、C、D四点不共面,且AB∥平面α,CD∥平面α,AC∩α=E,AD∩α=F,BD∩α=G,BC∩α=H,则四边形EFGH是( )
分析:要分析四边形EFGH的形状,可利用线面平行的判定和性质证出其两组对边的关系,从而得到四边形的形状.
解答:解:如图,
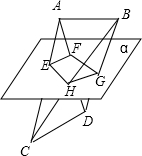
∵AC∩AD=A,∴AC与AD确定平面ACD,∵CD∥α,面ACD∩α=EF,∴EF∥CD,
∵BC∩BD=B,∴BC与BD确定平面BCD,∵CD∥α,面BCD∩α=GH,∴GH∥CD,
∴EF∥GH.
∵AC∩BC=C,∴AC与BC确定平面ACB,∵AB∥α,面ACB∩α=EH,∴EH∥AB,
∵BD∩AD=D,∴BD与AD确定平面ABD,∵AB∥α,面ABD∩α=GF,∴GF∥AB,
∴EH∥GF.
∴四边形EFGH是平行四边形.
故选A.

∵AC∩AD=A,∴AC与AD确定平面ACD,∵CD∥α,面ACD∩α=EF,∴EF∥CD,
∵BC∩BD=B,∴BC与BD确定平面BCD,∵CD∥α,面BCD∩α=GH,∴GH∥CD,
∴EF∥GH.
∵AC∩BC=C,∴AC与BC确定平面ACB,∵AB∥α,面ACB∩α=EH,∴EH∥AB,
∵BD∩AD=D,∴BD与AD确定平面ABD,∵AB∥α,面ABD∩α=GF,∴GF∥AB,
∴EH∥GF.
∴四边形EFGH是平行四边形.
故选A.
点评:本题考查了直线和平面平行的判定和性质,考查了学生的空间想象能力和思维能力,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
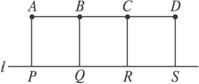
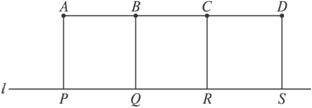
 如图,A、B、C、D是某煤矿的四个采煤点,l是公路,图中所标线段为道路,ABQP、BCRQ、CDSR近似于正方形.已知A、B、C、D四个采煤点每天的采煤量之比约为5:1:2:3,运煤的费用与运煤的路程、所运煤的重量都成正比.现要从P、Q、R、S中选出一处设立一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在( )
如图,A、B、C、D是某煤矿的四个采煤点,l是公路,图中所标线段为道路,ABQP、BCRQ、CDSR近似于正方形.已知A、B、C、D四个采煤点每天的采煤量之比约为5:1:2:3,运煤的费用与运煤的路程、所运煤的重量都成正比.现要从P、Q、R、S中选出一处设立一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在( )