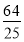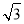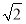题目内容
已知点A(－3,0)，B(3,0)，动点P满足|PA|＝2|PB|.
(1)若点P的轨迹为曲线C，求此曲线的方程；
(2)若点Q在直线l1：x＋y＋3＝0上，直线l2经过点Q且与曲线C只有一个公共点M，求|QM|的最小值．
（1）(x－5)2＋y2＝16（2）4
【解析】(1)设点P的坐标为(x，y)，且|PA|＝2|PB|，
则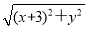
＝2
，
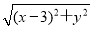化简得曲线C：(x－5)2＋y2＝16.
(2)曲线C是以点(5,0)为圆心，4为半径的圆，如图．
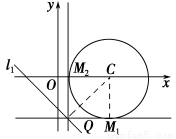
由直线l2是此圆的切线，连接CQ，
则|QM|＝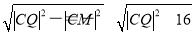
，
当CQ⊥l1时，|CQ|取最小值，|CQ|＝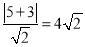
，此时|QM|的最小值为
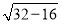＝4.
练习册系列答案
相关题目
