题目内容
已知圆(x－a)2＋(y－b)2＝r2的圆心为抛物线y2＝4x的焦点，且与直线3x＋4y＋2＝0相切，则该圆的方程为( )．
A．(x－1)2＋y2＝
B．x2＋(y－1)2＝
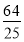
C．(x－1)2＋y2＝1 D．x2＋(y－1)2＝1
C
【解析】因为抛物线y2＝4x的焦点坐标为(1,0)，
所以a＝1，b＝0.又根据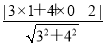
＝1＝r，
所以圆的方程为(x－1)2＋y2＝1.
练习册系列答案
相关题目
题目内容
已知圆(x－a)2＋(y－b)2＝r2的圆心为抛物线y2＝4x的焦点，且与直线3x＋4y＋2＝0相切，则该圆的方程为( )．
A．(x－1)2＋y2＝ B．x2＋(y－1)2＝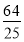
C．(x－1)2＋y2＝1 D．x2＋(y－1)2＝1
C
【解析】因为抛物线y2＝4x的焦点坐标为(1,0)，
所以a＝1，b＝0.又根据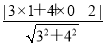＝1＝r，
所以圆的方程为(x－1)2＋y2＝1.
