题目内容
公差不为零的等差数列 的前
的前 项和为
项和为 ,若
,若 是
是 与
与 的等比中项,且
的等比中项,且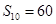 ,则
,则 =( )
=( )
 的前
的前 项和为
项和为 ,若
,若 是
是 与
与 的等比中项,且
的等比中项,且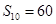 ,则
,则 =( )
=( )| A.80 | B.160 | C.320 | D.640 |
C
试题分析:公差不为零的等差数列{an}中,由a4是a3与a7的等比中项,S10=60,利用等差数列的通项公式和前n项和公式列方程组解得首项与公差,由此能求出S20. 解:∵a4是a3与a7的等比中项,S10=60,(a1+3d)2=(a1+2d)(a1+6d)∴10a1+45 d=60,∵公差不为零,∴解得a1=-3,d=2,∴S20=20a1+
 d=20×(-3)+190×2=320.故选C.
d=20×(-3)+190×2=320.故选C.点评:本题考查学生灵活运用等差数列的前n项和的公式及等比数列的通项公式化简求值,考查学生的计算能力,属于中档题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
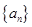 的首项为
的首项为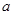 ,公差为
,公差为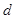 ,且不等式
,且不等式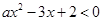 的解集为
的解集为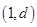 .
.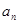 ;
;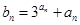 ,求数列
,求数列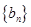 前
前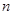 项和
项和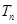 .
.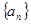 的前n项和为
的前n项和为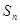 ,
,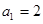 ,当n≥2时,
,当n≥2时,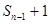 ,
,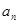 ,
,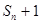 成等差数列. (1)求数列
成等差数列. (1)求数列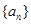 的通项公式;
的通项公式;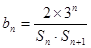 ,
,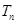 是数列
是数列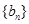 的前n项和,求使得
的前n项和,求使得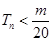 对所有
对所有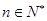 都成立的最小正整数
都成立的最小正整数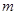 .
. ,则
,则 =_____________。
=_____________。 满足
满足 ,
,
 ;
; 项和
项和 ,并求当
,并求当 的前
的前 项和
项和 ,第
,第 项满足
项满足 ,则k=( )
,则k=( ) 的通项公式
的通项公式 ,其前
,其前 项和为
项和为 ,则
,则 等于( )
等于( ) 的各项都是正数,且满足:
的各项都是正数,且满足:
 ;
;