题目内容
已知:函数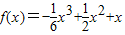 ,x∈R.
,x∈R.(Ⅰ)求证:函数f(x)的图象关于点
 中心对称,并求f(-2007)+f(-2006)+…+f(0)+f(1)+…+f(2009)的值.
中心对称,并求f(-2007)+f(-2006)+…+f(0)+f(1)+…+f(2009)的值.(Ⅱ)设g(x)=f′(x),an+1=g(an),n∈N+,且1<a1<2,求证:
(ⅰ)请用数学归纳法证明:当n≥2时,
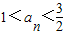 ;
;(ⅱ)
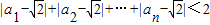 .
.
【答案】分析:(Ⅰ)设P(1-x1,y1)是函数f(x)的图象上的任一点,则P关于点 的对称点是Q(1+x1,
的对称点是Q(1+x1,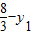 ),证明Q也在函数f(x)的图象上,即可得到结论;根据f(1+x1)+f(1-x1)=
),证明Q也在函数f(x)的图象上,即可得到结论;根据f(1+x1)+f(1-x1)= ,f(1)=
,f(1)= ,利用倒序相加法,即可求得结论;
,利用倒序相加法,即可求得结论;
(Ⅱ)g(x)=f′(x)=- .(ⅰ)先证明当n=2时,命题成立,再利用g(x)在[1,+∞)上单调递减,证明n=k+1时,命题成立,即可得到结论;
.(ⅰ)先证明当n=2时,命题成立,再利用g(x)在[1,+∞)上单调递减,证明n=k+1时,命题成立,即可得到结论;
(ⅱ)先证明 <
<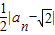 ,再利用等比数列的求和公式,即可得到结论.
,再利用等比数列的求和公式,即可得到结论.
解答:(Ⅰ)证明:设P(1-x1,y1)是函数f(x)的图象上的任一点,则P关于点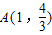 的对称点是Q(1+x1,
的对称点是Q(1+x1, )
)
∵f(1+x1)+f(1-x1)=[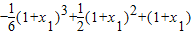 ]+[
]+[ ]=
]=
∴f(1+x1)= -f(1-x1)=
-f(1-x1)= -y1,
-y1,
∴Q也在函数f(x)的图象上
∴函数f(x)的图象关于点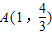 中心对称;
中心对称;
∵f(1+x1)+f(1-x1)= ,f(1)=
,f(1)=
∴f(-2007)+f(-2006)+…+f(0)+f(1)+…+f(2009)+f(2009)+f(2008)+…+f(2)+f(1)+…+f(-2007)=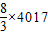
∴f(-2007)+f(-2006)+…+f(0)+f(1)+…+f(2009)=5356;
(Ⅱ)证明:g(x)=f′(x)=- .
.
(ⅰ)(1)当n=2时,a2=g(a1)=-
∵1<a1<2,∴1<a2< ,∴命题成立
,∴命题成立
(2)假设n=k(k≥2)时,1<ak< ,则ak+1=g(ak)=-
,则ak+1=g(ak)=-
∵g(x)在[1,+∞)上单调递减,∴1-g(2)<g( )<ak+1<g(1)=
)<ak+1<g(1)=
∴n=k+1时,命题成立
由(1)(2)可知,当n≥2时, ;
;
(ⅱ)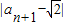 =
=


∵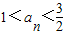 ,∴
,∴ <1
<1
∴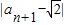 <
<
∴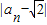 <
<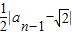 <…<
<…< <
<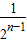
∴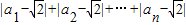 <1+
<1+ +…
+…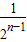 =2-
=2-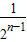 <2
<2
∴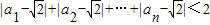 .
.
点评:本题考查函数图象的对称性,考查数学归纳法,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.
 的对称点是Q(1+x1,
的对称点是Q(1+x1,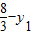 ),证明Q也在函数f(x)的图象上,即可得到结论;根据f(1+x1)+f(1-x1)=
),证明Q也在函数f(x)的图象上,即可得到结论;根据f(1+x1)+f(1-x1)= ,f(1)=
,f(1)= ,利用倒序相加法,即可求得结论;
,利用倒序相加法,即可求得结论;(Ⅱ)g(x)=f′(x)=-
 .(ⅰ)先证明当n=2时,命题成立,再利用g(x)在[1,+∞)上单调递减,证明n=k+1时,命题成立,即可得到结论;
.(ⅰ)先证明当n=2时,命题成立,再利用g(x)在[1,+∞)上单调递减,证明n=k+1时,命题成立,即可得到结论;(ⅱ)先证明
 <
<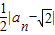 ,再利用等比数列的求和公式,即可得到结论.
,再利用等比数列的求和公式,即可得到结论.解答:(Ⅰ)证明:设P(1-x1,y1)是函数f(x)的图象上的任一点,则P关于点
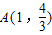 的对称点是Q(1+x1,
的对称点是Q(1+x1, )
)∵f(1+x1)+f(1-x1)=[
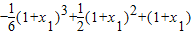 ]+[
]+[ ]=
]=
∴f(1+x1)=
 -f(1-x1)=
-f(1-x1)= -y1,
-y1,∴Q也在函数f(x)的图象上
∴函数f(x)的图象关于点
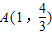 中心对称;
中心对称;∵f(1+x1)+f(1-x1)=
 ,f(1)=
,f(1)=
∴f(-2007)+f(-2006)+…+f(0)+f(1)+…+f(2009)+f(2009)+f(2008)+…+f(2)+f(1)+…+f(-2007)=
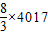
∴f(-2007)+f(-2006)+…+f(0)+f(1)+…+f(2009)=5356;
(Ⅱ)证明:g(x)=f′(x)=-
 .
.(ⅰ)(1)当n=2时,a2=g(a1)=-

∵1<a1<2,∴1<a2<
 ,∴命题成立
,∴命题成立(2)假设n=k(k≥2)时,1<ak<
 ,则ak+1=g(ak)=-
,则ak+1=g(ak)=-
∵g(x)在[1,+∞)上单调递减,∴1-g(2)<g(
 )<ak+1<g(1)=
)<ak+1<g(1)=
∴n=k+1时,命题成立
由(1)(2)可知,当n≥2时,
 ;
;(ⅱ)
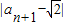 =
=


∵
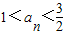 ,∴
,∴ <1
<1∴
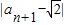 <
<
∴
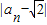 <
<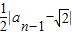 <…<
<…< <
<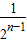
∴
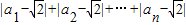 <1+
<1+ +…
+…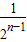 =2-
=2-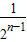 <2
<2∴
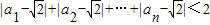 .
.点评:本题考查函数图象的对称性,考查数学归纳法,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
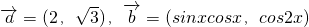 ,函数
,函数 (x∈R).
(x∈R).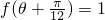 ,求tan2θ的值.
,求tan2θ的值.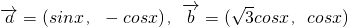 ,函数
,函数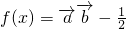 ,x∈R.
,x∈R.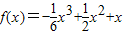 ,x∈R.
,x∈R. 中心对称,并求f(-2007)+f(-2006)+…+f(0)+f(1)+…+f(2009)的值.
中心对称,并求f(-2007)+f(-2006)+…+f(0)+f(1)+…+f(2009)的值.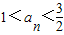 ;
;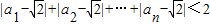 .
.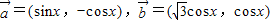 ,函数
,函数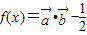 ,x∈R.
,x∈R.