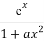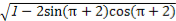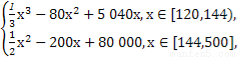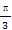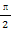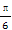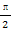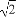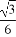Question

关于函数f(x)=4sin(2x+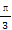)(x∈R),有下列命题:

①由f(x1)=f(x2)=0可得x1-x2必是π的整数倍;

②y=f(x)的表达式可改写为y=4 cos(2x-);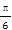

③y=f(x)的图象关于点(-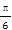,0)对称;

④y=f(x)的图象关于直线x=-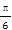对称.

其中正确命题的序号是　　　.

 

Answer 1

②③

【解析】①错,∵当x1=-,x2=时,f(x1)=f(x2)=0,而x1-x2=-.

②对,∵y=4cos(2x-)=4cos[-(2x+)]

=4sin(2x+).

③对,∵当x=-时,2x+=0,此时f(x)=0,

故f(x)的图象关于(-,0)成中心对称.

④错,由③可知x=-不是y=f(x)的图象的对称轴.