题目内容
6.下列各组向量中,可以作为基底的是( )| A. | $\overrightarrow{e_1}=(0,0),\overrightarrow{e_2}=(1,-2)$ | B. | $\overrightarrow{e_1}=(-1,2),\overrightarrow{e_2}=(5,7)$ | ||
| C. | $\overrightarrow{e_1}=(3,5),\overrightarrow{e_2}=(6,10)$ | D. | $\overrightarrow{e_1}=(\frac{1}{2},-\frac{3}{4}),\overrightarrow{e_2}=(2,-3)$ |
分析 判断两个向量是否共线,即可得到结果.
解答 解:向量$\overrightarrow{{e}_{1}}=(0,0),\overrightarrow{{e}_{2}}=(1,-2)$是共线向量,A不正确;
$\overrightarrow{{e}_{1}}=(-1,2),\overrightarrow{{e}_{2}}=(5,7)$是不共线向量,可以是基底,B正确;
$\overrightarrow{{e}_{1}}=(3,5),\overrightarrow{{e}_{2}}=(6,10)$是共线向量,C不正确;
$\overrightarrow{{e}_{1}}=(\frac{1}{2},-\frac{3}{4}),\overrightarrow{{e}_{2}}=(2,-3)$是共线向量,D不正确;
故选:B.
点评 本题考查向量共线以及向量基本定理的应用,是基础题.

练习册系列答案
相关题目
16.若x0是函数 f(x)=lgx+x-2的一个零点,则x0属于区间( )
| A. | (0,1) | B. | (1,1.5) | C. | (1.5,2) | D. | (2,2.5) |
17.等比数列{an}中,a2a4=$\frac{1}{2}$,则a1a32a5=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
1.已知函数y=Asin(ωx+φ)(x∈R)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,则( )
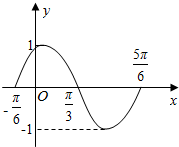

| A. | y=sin(x-$\frac{π}{6}$) | B. | y=sin(2x+$\frac{π}{3}$) | C. | y=-sin(2x+$\frac{π}{6}$) | D. | y=sin(2x+$\frac{π}{6}$) |
11.设c,b是两条直线,α,β是两个平面,下列能推出c⊥b的是( )
| A. | c⊥α,b∥β,α⊥β | B. | c⊥α,b⊥β,α∥β | C. | c?α,b⊥β,α∥β | D. | c?α,b∥β,α⊥β |