题目内容
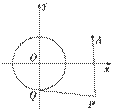
已知圆O:x2+y2=8交x轴于A,B两点,曲线C是以AB为长轴,直线:x=-4为准线的椭圆.
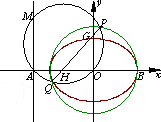
(1)求椭圆的标准方程;
(2)若M是直线上的任意一点,以OM为直径的圆K与圆O相交于P,Q两点,求证:直线PQ必过定点E,并求出点E的坐标;
(3)如图所示,若直线PQ与椭圆C交于G,H两点,且![]() ,试求此时弦PQ的长.
,试求此时弦PQ的长.
答案:
解析:
解析:
|
解:(Ⅰ)设椭圆的标准方程为 (Ⅱ)设 (Ⅲ)解法一:设 代入①解得: 从而圆心 从而 解法二:过点 由 由此直线PQ的方程为 解法三:将 消去 所以 |

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 ,从而:
,从而: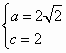 ,故
,故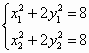 ,①
,①
 (舍去正值),
(舍去正值), (Ⅲ)给出定点M(0,2),设P、Q分别为直线l和圆O上动点,求|MP|+|PQ|的最小值及此时点P的坐标.
(Ⅲ)给出定点M(0,2),设P、Q分别为直线l和圆O上动点,求|MP|+|PQ|的最小值及此时点P的坐标.