Question

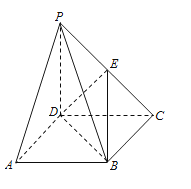
【题目】(2015·江苏）如图，在直三棱柱ABC-A1B1C1中，已知AC⊥BC，BC=CC1 ， 设AB1的中点为D，B1CBC1=E.求证:

（1）DE∥平面AA1C1C
（2）BC1⊥AB1

Answer 1

【答案】
（1）

见解析。

（2）

见解析。

【解析】由三棱锥性质知侧面BB1C1C为平行四边形,因此点E为B1C的中点，从而由三角形中位线性质得DE∥AC,，再由线面平行判定定理得DE∥平面AA1C1C（2）因为直三棱柱ABC-A1B1C1中，BC=CC1所以侧面BB1C1C为正方形，因此BC1⊥B1C，又，AC⊥BC, AC⊥CC1（可由直三棱柱推导），因此由线面垂直判定定理得AC⊥平面BB1C1C,从而AC⊥BC1 ， 再由线面垂直判定定理得BC1⊥平面AB1C, 进而可得BC1⊥AB1.
（1）由题意知，E为B1C的中点，又D为A1B的中点，因此DE∥AC。 又因为DE平面AA1C1C, AC平面AA1C1C，所以DE∥平面AA1C1C。
（2）因为棱柱ABC-A1B1C1是直三棱柱， 所以CC1⊥平面ABC， 所以AC⊥CC1，又因为AC⊥BC, CC1平面BCC1B1 ， BCBCC1B1, BCCC1=C,
所以AC⊥平面BCC1B1 ， 又因为BC1BCC1B1， 所以BC1⊥B1C.
因为AC, B1C平面B1AC, AC1C=C, 所以BC1⊥平面B1AC。 又因为AB1平面B1AC， 所以BC1⊥AB1。

【考点精析】本题主要考查了直线与平面平行的判定的相关知识点，需要掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行才能正确解答此题．