题目内容
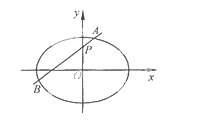
【题目】(2015·四川）如图，椭圆E：
的离心率是
，点P（0,1）在短轴CD上， 且
.
（1）求椭圆E的方程；
（2）设O为坐标原点，过点P的动直线与椭圆交于A、B两点.是否存在常数λ ， 使得
为定值？若存在，求λ的值；若不存在，请说明理由.
【答案】
（1）
.
（2）
在常数λ＝－1，使得
为定值－3.
【解析】
(I)由已知，点C，D的坐标分别为(0，－b)，(0，b)
又点P的坐标为(0，1)，且2＋λ[x1x2＋(y1－1)(y2－1)]
＝(1＋λ)(1＋k2)x1x2＋k(x1＋x2)＋1
＝
＝－
-
-2
所以，当λ＝1时，－＝－3
此时，B即为直线CD
此时
=
＝－2－1＝－3
故存在常数λ＝－1，使得为定值－3.
【考点精析】通过灵活运用椭圆的标准方程，掌握椭圆标准方程焦点在x轴：
，焦点在y轴：即可以解答此题．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
