题目内容
(本小题12分)
某工厂用两种不同原料可生产同一产品,若采用甲种原料,每吨成本1000元,运费500元,可得产品90kg; 若采用乙种原料,每吨成本1500元,运费400元,可得产品100kg,如果每月原料的总成本不超过6000元,运费不超过2000元,那么如何分配甲乙两种原料使此工厂每月生产的产品最多?最多是多少千克?
某工厂用两种不同原料可生产同一产品,若采用甲种原料,每吨成本1000元,运费500元,可得产品90kg; 若采用乙种原料,每吨成本1500元,运费400元,可得产品100kg,如果每月原料的总成本不超过6000元,运费不超过2000元,那么如何分配甲乙两种原料使此工厂每月生产的产品最多?最多是多少千克?
工厂每月最多可生产440千克产品。
试题分析:设工厂每月用甲种原料x吨,乙种原料y吨,可生产z千克产品,然后列出x,y满足的不等式组,写出目标函数,从而转化为线性规划问题来解,然后作出可行域,找出最优解。.
工厂每月用甲种原料x吨,乙种原料y吨,可生产z千克产品,………………1分
则
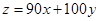 ,……………2分
,……………2分且
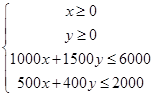 即
即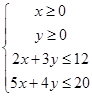 …………………5分
…………………5分作出以上不等式组所表示的平面区域(图略)画完图………………………7分
由
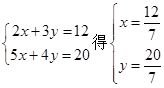 ………………9分
………………9分令
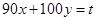 ,作出直线:
,作出直线: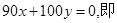
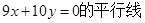
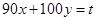
当
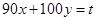 过点
过点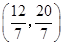 时,直线
时,直线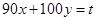 的截距最大,由此得
的截距最大,由此得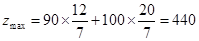 ………………11分
………………11分答:工厂每月最多可生产440千克产品。……………………12分
点评:读懂题意正确建立数学模型是解决此类问题的关键,本题属于线性规划问题,要注意正确作出可行域,是找最优解的关键。

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
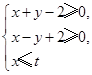 若目标函数
若目标函数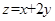 的最大值是10,则实数
的最大值是10,则实数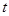 的值为
的值为 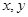 满足
满足 则
则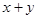 的最小值是
的最小值是 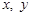 满足
满足 ,则
,则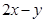 的最小值为 .
的最小值为 .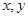 满足约束条件
满足约束条件 ,则
,则 的最大值为 ( )
的最大值为 ( )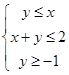 下,过点
下,过点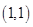 目标函数
目标函数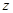 取得最大值10,则目标函数
取得最大值10,则目标函数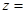 ______(写出一个适合题意的目标函数即可);
______(写出一个适合题意的目标函数即可);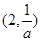 在直线
在直线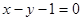 的左上方,则实数
的左上方,则实数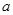 的取值范围是
的取值范围是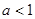
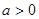

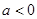 或
或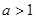
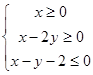 ,则
,则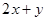 的最小值为__________ -
的最小值为__________ -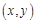 满足
满足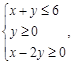 则
则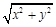 的最大值为( )
的最大值为( )