题目内容
抛物线 在点P处的切线
在点P处的切线 分别交x轴、y轴于不同的两点A、B,
分别交x轴、y轴于不同的两点A、B, 。当点P在C上移动时,点M的轨迹为D。
。当点P在C上移动时,点M的轨迹为D。
(1)求曲线D的方程:
(2)圆心E在y轴上的圆与直线 相切于点P,当|PE|=|PA|,求圆的方程。
相切于点P,当|PE|=|PA|,求圆的方程。
【答案】
(Ⅰ)y=-3x2(x≠0) (Ⅱ)
【解析】本试题主要是考查了轨迹方程的求解以及直线与圆的位置关系的运用。利用向量的知识表示出轨迹方程,以及设出直线方程,利用圆心E在y轴上的圆与直线 相切于点P,当|PE|=|PA|得到结论。
相切于点P,当|PE|=|PA|得到结论。
(1)利用 的关系式,设出坐标,然后代入得到消去参数得到轨迹方程。
的关系式,设出坐标,然后代入得到消去参数得到轨迹方程。
(2)利用圆心E在y轴上的圆与直线 相切于点P,当|PE|=|PA|得到结论。
相切于点P,当|PE|=|PA|得到结论。
解:
(Ⅰ)对y=x2求导,得y¢=2x.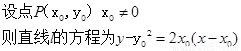
在l方程中分别令y=0,x=0,得 …3分
…3分
设M(x,y), 由此得x0=3x,
由此得x0=3x, =-3y,
=-3y,
消去x0,得曲线D的方程为y=-3x2(x≠0). …6分
(Ⅱ)依题意,直线PE方程为y-


练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目