题目内容
2.已知点A(1,-1),B(3,0),C(2,1).若平面区域D由所有满足$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$(1≤λ≤2,0≤μ≤1)的点P组成,则D的面积为3.分析 如图所示,点P组成的图形是以BD、BF为邻边的平行四边形,利用两个向量的数量积的定义,求出cos∠FBD=cos∠CAB的值,可得sin∠CAB的值,再根据所求面积为BD•BF•sin∠CAB,计算求得结果.
解答 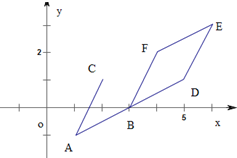 解:如图:延长AB到D,使BD=AB,作BF平行且等于AC,
解:如图:延长AB到D,使BD=AB,作BF平行且等于AC,
则点P组成的图形是以BD、BF为邻边的平行四边形,
又BD=AB=$\sqrt{5}$,BF=AC=$\sqrt{5}$,cos∠FBD=cos∠CAB
=$\frac{{\overrightarrow{AC}•\overrightarrow{AB}}}{{|{\overrightarrow{AC}}||{\overrightarrow{AB}}|}}=\frac{{({1,2})•({2,1})}}{{{{({\sqrt{5}})}^2}}}=\frac{4}{5}$,
所以$sin∠FBD=\sqrt{1-{{cos}^2}∠FBD}=\frac{3}{5}$,
故所以所求面积为:$|{BD}||{BF}|sin∠FBD={({\sqrt{5}})^2}•\frac{3}{5}=3$,
故答案为:3.
点评 本题主要考查平面向量基本定理,数量积表示两个两个向量的夹角,体现了数形结合的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.在锐角△ABC中,若A=2B,则$\frac{a}{b}$的范围是( )
| A. | ($\sqrt{2}$,$\sqrt{3}$) | B. | ($\sqrt{3}$,2) | C. | (0,2) | D. | ($\sqrt{2}$,2) |
17.如图所示的三个直角三角形是一个体积为20cm3的几何体的三视图,则h=( )cm.


| A. | 4 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
11.计算:$\frac{1-2si{n}^{2}α}{2co{s}^{2}α-1}$=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |