ƒøƒ⁄»ð
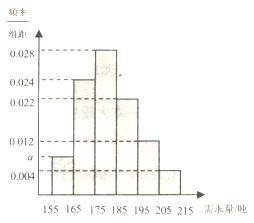
°æƒø°øŒ™¡ÀΩ‚–°—ß…˙µƒÃƒЫÈøˆ£¨œ÷≥È»°ƒ≥–°—ß¡˘ƒÍº∂100√˚—ß…˙Ω¯––ï…˛≤‚ ‘£¨π€≤Ϻ«¬º∫¢◊”√«»˝∑÷÷”ƒ⁄µƒÃ¯…˛∏ˆ ˝£¨Ω´À˘µ√µƒ ˝æð’˚¿Ì∫Ûª≠≥ˆ∆µ¬ ∑÷≤º÷±∑ΩÕº£¨Ã¯…˛∏ˆ ˝µƒ ˝÷µ¬‰‘⁄«¯º‰![]() £¨
£¨![]() £¨
£¨![]() ƒ⁄µƒ∆µ¬ ÷Ʊ»Œ™
ƒ⁄µƒ∆µ¬ ÷Ʊ»Œ™![]() .£®º∆À„Ω·π˚±£¡Ù–° ˝µ„∫Û√Ê3Œª£©
.£®º∆À„Ω·π˚±£¡Ù–° ˝µ„∫Û√Ê3Œª£©

£®¢Ò£©«Û’‚–©—ß…˙ï…˛∏ˆ ˝µƒ ˝÷µ¬‰‘⁄«¯º‰![]() ƒ⁄µƒ∆µ¬ £ª
ƒ⁄µƒ∆µ¬ £ª
£®¢Ú£©”√∑÷≤„≥È—˘µƒ∑Ω∑®‘⁄«¯º‰![]() ƒ⁄≥È»°“ª∏ˆ»ð¡øŒ™6µƒ—˘±æ£¨Ω´∏√—˘±æø¥≥…“ª∏ˆ◊Ð㨥”÷–»Œ“‚—°»°2∏ˆ—ß…˙£¨«Û’‚2∏ˆ—ß…˙ï…˛∏ˆ ˝µƒ ˝÷µ∂º‘⁄«¯º‰
ƒ⁄≥È»°“ª∏ˆ»ð¡øŒ™6µƒ—˘±æ£¨Ω´∏√—˘±æø¥≥…“ª∏ˆ◊Ð㨥”÷–»Œ“‚—°»°2∏ˆ—ß…˙£¨«Û’‚2∏ˆ—ß…˙ï…˛∏ˆ ˝µƒ ˝÷µ∂º‘⁄«¯º‰![]() ƒ⁄µƒ∏≈¬ .
ƒ⁄µƒ∏≈¬ .
°æ¥∞∏°ø£®¢Ò£©0.05£ª£®¢Ú£©![]() .
.
°æΩ‚Œˆ°ø
£®¢Ò£©∏˘æð∆µ¬ ÷Ʊ»£¨ø…ºŸ…Ë ˝÷µ¬‰‘⁄«¯º‰![]() £¨
£¨![]() £¨
£¨![]() µƒ∆µ¬ £¨»ª∫Û¿˚”√À˘”–∆µ¬ ÷Æ∫ÕŒ™1£¨ø…µ√Ω·π˚.
µƒ∆µ¬ £¨»ª∫Û¿˚”√À˘”–∆µ¬ ÷Æ∫ÕŒ™1£¨ø…µ√Ω·π˚.
£®¢Ú£©∏˘æ𫯺‰![]() £¨
£¨![]() £¨
£¨![]() ƒ⁄µƒ∆µ¬ ÷Ʊ»Œ™£∫3£∫2£∫1£¨∞¥∑÷≤„≥È—˘µƒ∑Ω∑®Ω´’‚»˝∏ˆ«¯º‰µƒÀ˘≥È»°µƒ»À ˝∑÷±Ω¯––±Í∫≈£¨≤…”√¡–æŸ∑®£¨»ª∫Û¿˚”√π≈µ‰∏≈–Õ£¨ø…µ√Ω·π˚.
ƒ⁄µƒ∆µ¬ ÷Ʊ»Œ™£∫3£∫2£∫1£¨∞¥∑÷≤„≥È—˘µƒ∑Ω∑®Ω´’‚»˝∏ˆ«¯º‰µƒÀ˘≥È»°µƒ»À ˝∑÷±Ω¯––±Í∫≈£¨≤…”√¡–æŸ∑®£¨»ª∫Û¿˚”√π≈µ‰∏≈–Õ£¨ø…µ√Ω·π˚.
£®¢Ò£©…Ë«¯º‰![]() ƒ⁄µƒ∆µ¬ Œ™
ƒ⁄µƒ∆µ¬ Œ™![]() £¨‘Ú«¯º‰
£¨‘Ú«¯º‰![]() £¨
£¨![]() ƒ⁄µƒ∆µ¬ ∑÷±Œ™
ƒ⁄µƒ∆µ¬ ∑÷±Œ™![]() ∫Õ
∫Õ![]() £¨“¿Ã‚“‚µ√£∫
£¨“¿Ã‚“‚µ√£∫ ![]() .Ω‚µ√
.Ω‚µ√![]() .
.
À˘“‘«¯º‰![]() ƒ⁄µƒ∆µ¬ Œ™0.05.
ƒ⁄µƒ∆µ¬ Œ™0.05.
£®¢Ú£©”…£®¢Ò£©µ√£∫«¯º‰![]() £¨
£¨![]() £¨
£¨![]() ƒ⁄µƒ∆µ¬ “¿¥ŒŒ™0.3£¨0.2£¨0.1.
ƒ⁄µƒ∆µ¬ “¿¥ŒŒ™0.3£¨0.2£¨0.1.
”√∑÷≤„≥È—˘µƒ∑Ω∑®‘⁄«¯º‰![]() ƒ⁄≥È»°“ª∏ˆ»ð¡øŒ™6µƒ—˘±æ.
ƒ⁄≥È»°“ª∏ˆ»ð¡øŒ™6µƒ—˘±æ.
‘Ú‘⁄«¯º‰![]() ƒ⁄”¶≥È»°
ƒ⁄”¶≥È»°![]() »À£¨º«Œ™
»À£¨º«Œ™![]() £¨
£¨![]() £¨
£¨![]()
‘⁄«¯º‰![]() ƒ⁄”¶≥È»°
ƒ⁄”¶≥È»°![]() »À£¨º«Œ™
»À£¨º«Œ™![]() £¨
£¨![]() £¨
£¨
‘⁄«¯º‰![]() ƒ⁄”¶≥È»°
ƒ⁄”¶≥È»°![]() »À£¨º«Œ™
»À£¨º«Œ™![]() .
.
…Ë°∞¥”÷–»Œ“‚—°»°2∏ˆ∫¢◊”£¨’‚2∏ˆ∫¢◊”ï…˛ ˝÷µ∂º‘⁄«¯º‰![]() ƒ⁄°±Œ™ ¬º˛
ƒ⁄°±Œ™ ¬º˛![]() £¨
£¨
‘ÚÀ˘”–µƒª˘±æ ¬º˛”–£∫
![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨π≤15÷÷.
£¨π≤15÷÷.
¬º˛![]() ∞¸∫¨µƒª˘±æ ¬º˛”–£∫
∞¸∫¨µƒª˘±æ ¬º˛”–£∫
![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
![]() £¨
£¨![]() £¨π≤10÷÷.
£¨π≤10÷÷.
À˘“‘’‚2∏ˆ∫¢◊”ï…˛ ˝÷µ∂º‘⁄«¯º‰![]() ƒ⁄µƒ∏≈¬ Œ™
ƒ⁄µƒ∏≈¬ Œ™![]() .
.