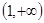题目内容
己知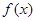 为定义域为 R 内的减函数,且
为定义域为 R 内的减函数,且
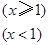 , 则实数
, 则实数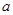 的取值范围为 .
的取值范围为 .
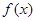 为定义域为 R 内的减函数,且
为定义域为 R 内的减函数,且
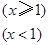 , 则实数
, 则实数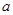 的取值范围为 .
的取值范围为 .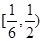
试题分析:根据题意,由于
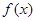 为定义域为 R 内的减函数,且解析式为
为定义域为 R 内的减函数,且解析式为
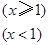 ,,则说明2a-1>0,a>1,同时在x=1时,左边的函数值大于等于右边的函数值,即可知
,,则说明2a-1>0,a>1,同时在x=1时,左边的函数值大于等于右边的函数值,即可知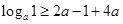 ,故可知解得实数
,故可知解得实数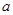 的取值范围为
的取值范围为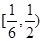 ,答案为
,答案为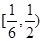 。
。点评:主要是考查了分段函数单调性的运用,属于基础题

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
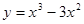 在
在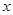 等于 处取得极小值.
等于 处取得极小值.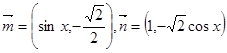 ,函数
,函数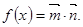
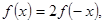 求
求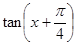 的值;
的值;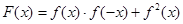 的最大值和单调递增区间。
的最大值和单调递增区间。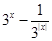 .
.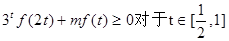 恒成立,求m的取值范围。
恒成立,求m的取值范围。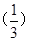 <f
<f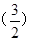 <
<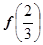
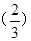 <f
<f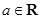 ,函数
,函数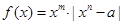 .
.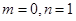 ,写出函数
,写出函数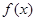 的单调递增区间(不必证明);
的单调递增区间(不必证明);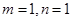 ,当
,当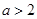 时,求函数
时,求函数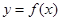 在区间
在区间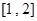 上的最小值.
上的最小值.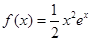 .
.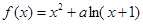 有两个极值点
有两个极值点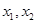 ,且
,且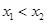 .
.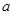 的取值范围;
的取值范围;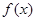 的单调性;
的单调性;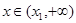 ,都有
,都有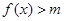 成立,求实数
成立,求实数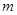 的取值范围.
的取值范围.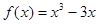 的递减区间是
的递减区间是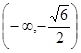 或
或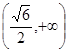
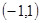
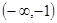 或
或