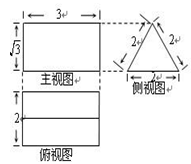
题目内容
若正方体的棱长为 ,则以该正方体各个面的中心为顶点的凸多面体的体积为 ( )
,则以该正方体各个面的中心为顶点的凸多面体的体积为 ( )
 ,则以该正方体各个面的中心为顶点的凸多面体的体积为 ( )
,则以该正方体各个面的中心为顶点的凸多面体的体积为 ( )A. | B. | C. | D. |
B
试题分析:解:所求八面体体积是两个底面边长为1,高为
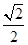 , 的四棱锥的体积和,一个四棱锥体积V1=
, 的四棱锥的体积和,一个四棱锥体积V1=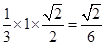 ,故八面体体积V=2V1=
,故八面体体积V=2V1= ,故选B.
,故选B.点评:本题是基础题,开心棱锥的体积,正方体的内接多面体,体积的求法常用转化思想,变为易求的几何体的体积,考查计算能力

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目




 ),则该棱锥的体积是
),则该棱锥的体积是 





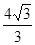

 内的射影构成的图形面积的取值范围是( )
内的射影构成的图形面积的取值范围是( )



 的底面边长为2,
的底面边长为2, .
.
 为线段
为线段 的中点,求
的中点,求 与平面
与平面 所成角的大小.
所成角的大小.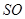 中,
中,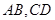 为底面圆的两条直径 ,AB交CD于O,且
为底面圆的两条直径 ,AB交CD于O,且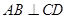 ,
,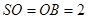 ,
,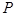 为
为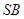 的中点.
的中点.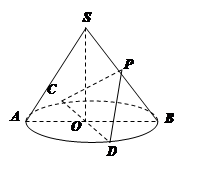
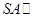 平面
平面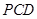 ;
;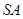 与
与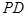 所成角的正切值 .
所成角的正切值 .