题目内容
(1)已知△ABC中,角A,B,C的对边分别是a,b,c,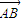 •
•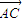 =3,a=2
=3,a=2 ,b+c=6,求cosA.
,b+c=6,求cosA.(2)设f(x)=-2cos2
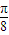 x+sin(
x+sin(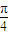 x-
x-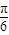 )+1,y=g(x)与y=f(x)的图象关于直线x=1对称,当x∈[-
)+1,y=g(x)与y=f(x)的图象关于直线x=1对称,当x∈[- ,0]时,求y=g(x)的最大值.
,0]时,求y=g(x)的最大值.
【答案】分析:(1)由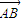 •
• =3,可得 bc•cosA=3,再由余弦定理求得 bc=5,由此求得 cosA=
=3,可得 bc•cosA=3,再由余弦定理求得 bc=5,由此求得 cosA=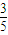 .
.
(2)由三角函数的恒等变换及化简求值可得f(x)=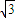 sin(
sin(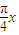 -
-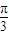 ),根据对称性可得 g(x)=f(2-x)=
),根据对称性可得 g(x)=f(2-x)=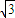 cos(
cos(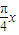 +
+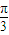 ),再由x∈[-
),再由x∈[- ,0],求得
,0],求得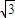 cos(
cos(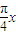 +
+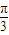 )的最大值,
)的最大值,
即为所求.
解答:解:(1)∵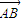 •
•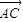 =3,∴bc•cosA=3. (1分)
=3,∴bc•cosA=3. (1分)
又 a2=b2+c2-2bc•cosA=(b+c)2-2bc-2bc•cosA,即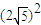 =62-2bc-2×3,∴bc=5,(5分)
=62-2bc-2×3,∴bc=5,(5分)
∴cosA=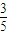 . (6分)
. (6分)
(2)f(x)=-2cos2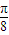 x+sin(
x+sin(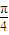 x-
x-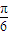 )+1=sin
)+1=sin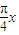 cos
cos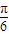 -cos
-cos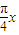 sin
sin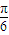 -cos
-cos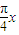 =
=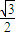 sin
sin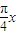 -
- cos
cos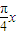 =
= sin(
sin( -
-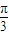 ).(8分)
).(8分)
∵y=g(x)与y=f(x)的图象关于直线x=1对称,
∴g(x)=f(2-x)=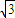 sin[
sin[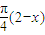 -
-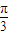 ]=
]=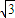 cos(
cos(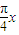 +
+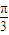 ). (10分)
). (10分)
∵x∈[- ,0],∴
,0],∴ ≤(
≤(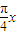 +
+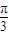 )≤
)≤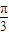 ,
,
∴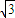 cos(
cos(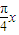 +
+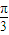 )的最大值为
)的最大值为 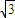 ×
×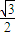 =
= ,即 当x∈[-
,即 当x∈[- ,0]时,求y=g(x)的最大值为
,0]时,求y=g(x)的最大值为  .(12分)
.(12分)
点评:本题主要考查三角函数的恒等变换及化简求值,余弦定理的应用,正弦函数的定义域和值域,属于中档题.
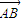 •
• =3,可得 bc•cosA=3,再由余弦定理求得 bc=5,由此求得 cosA=
=3,可得 bc•cosA=3,再由余弦定理求得 bc=5,由此求得 cosA=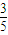 .
. (2)由三角函数的恒等变换及化简求值可得f(x)=
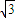 sin(
sin(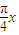 -
-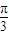 ),根据对称性可得 g(x)=f(2-x)=
),根据对称性可得 g(x)=f(2-x)=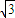 cos(
cos(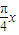 +
+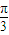 ),再由x∈[-
),再由x∈[- ,0],求得
,0],求得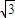 cos(
cos(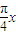 +
+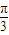 )的最大值,
)的最大值,即为所求.
解答:解:(1)∵
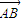 •
•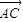 =3,∴bc•cosA=3. (1分)
=3,∴bc•cosA=3. (1分)又 a2=b2+c2-2bc•cosA=(b+c)2-2bc-2bc•cosA,即
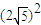 =62-2bc-2×3,∴bc=5,(5分)
=62-2bc-2×3,∴bc=5,(5分)∴cosA=
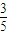 . (6分)
. (6分)(2)f(x)=-2cos2
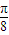 x+sin(
x+sin(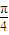 x-
x-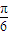 )+1=sin
)+1=sin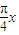 cos
cos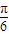 -cos
-cos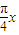 sin
sin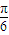 -cos
-cos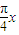 =
=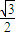 sin
sin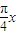 -
- cos
cos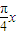 =
= sin(
sin( -
-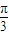 ).(8分)
).(8分)∵y=g(x)与y=f(x)的图象关于直线x=1对称,
∴g(x)=f(2-x)=
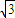 sin[
sin[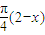 -
-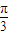 ]=
]=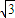 cos(
cos(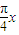 +
+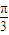 ). (10分)
). (10分)∵x∈[-
 ,0],∴
,0],∴ ≤(
≤(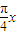 +
+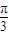 )≤
)≤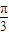 ,
,∴
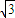 cos(
cos(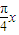 +
+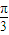 )的最大值为
)的最大值为 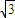 ×
×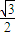 =
= ,即 当x∈[-
,即 当x∈[- ,0]时,求y=g(x)的最大值为
,0]时,求y=g(x)的最大值为  .(12分)
.(12分)点评:本题主要考查三角函数的恒等变换及化简求值,余弦定理的应用,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目