题目内容
已知定义在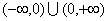 上的函数
上的函数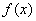 满足
满足
①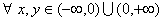 ,
,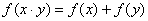 ;
;
②当 时,
时, ,且
,且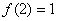 。
。
(1)试判断函数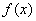 的奇偶性;
的奇偶性;
(2)判断函数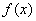 在(0,+∞)上的单调性;
在(0,+∞)上的单调性;
(3)求函数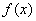 在区间
在区间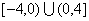 上的最大值;
上的最大值;
(4)求不等式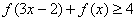 的解集。
的解集。
【答案】
(1)令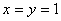 ,则
,则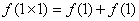 ,得
,得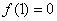 ;
;
再令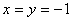 ,则
,则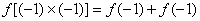 ,得
,得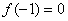 .
.
对于条件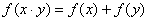 ,令
,令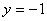 ,
,
则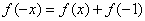 ,所以
,所以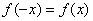 。
。
又函数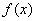 的定义域关于原点对称,所以函数
的定义域关于原点对称,所以函数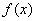 为偶函数。…………3分
为偶函数。…………3分
(2)任取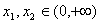 ,且
,且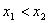 ,则有
,则有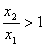 .
.
又∵当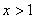 时,
时,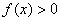 ,∴
,∴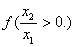
而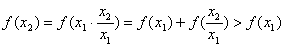 ,
,
所以函数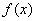 在(0,+∞)上是增函数。 ………………6分
在(0,+∞)上是增函数。 ………………6分
(3)∵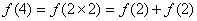 ,又
,又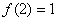 ,
,
∴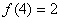 .
.
又由(1)知函数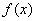 在区间
在区间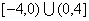 上是偶函数且在
上是偶函数且在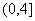 上是增函数,
上是增函数,
∴函数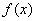 在区间
在区间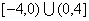 上的最大值为
上的最大值为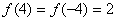 …………9分
…………9分
(4)∵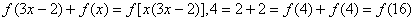
∴原不等式等价于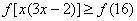
又函数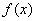 为偶函数,且函数
为偶函数,且函数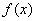 在
在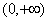 上是增函数,
上是增函数,
∴原不等式又等价于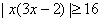 ,
,
即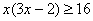 或
或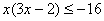 ,
,
∴不等式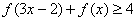 的解集为
的解集为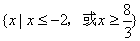 ………………12分
………………12分

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目






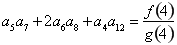

 上的函数
上的函数 满足
满足 ,当
,当 时,
时, ,若函数
,若函数 至少有6个零点,则
至少有6个零点,则 的取值范围是
( )
的取值范围是
( ) B.
B.
 D.
D.
 上的函数
上的函数 满足
满足 ,且
,且 ,
,
 ,若有穷数列
,若有穷数列 (
( )的前
)的前 项和等于
项和等于 ,则
,则 上的函数
上的函数 满足
满足 ,且
,且
 ,若有穷数列
,若有穷数列 (
( )的前
)的前 项和等于
项和等于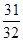 ,则
,则 上的函数
上的函数 满足
满足 ,且
,且 ,
,  ,若有穷数列
,若有穷数列 (
(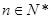 )的前
)的前 项和等于
项和等于 ,则n等于
,则n等于