题目内容
(本题满分12分)
两条互相平行的直线分别过点A(6,2)和B(-3,-1),并且各自绕着A,B旋转,如果两条平行直线间的距离为d.
求:1)d的变化范围;
2)当d取最大值时两条直线的方程.
两条互相平行的直线分别过点A(6,2)和B(-3,-1),并且各自绕着A,B旋转,如果两条平行直线间的距离为d.
求:1)d的变化范围;
2)当d取最大值时两条直线的方程.
(1) (0,3].(2) 3x+y-20=0和3x+y+10=0.
(1)两直线的最大距离为直线与线段AB垂直时,距离最大,最大值为|AB|= .所以d的变化范围为
.所以d的变化范围为 .
.
(2)由于当d最大时,AB与直线垂直,所以可以利用AB的斜率求出直线的斜率,进而求出其直线方程.
(1)方法一:①当两条直线的斜率不存在时,即两直线分别为x=6和x=-3,则它们之间的距离为9. ………………2分
②当两条直线的斜率存在时,设这两条直线方程为
l1:y-2=k(x-6),l2:y+1=k(x+3),
即l1:kx-y-6k+2=0,l2:kx-y+3k-1=0, ………………4分
∴d==. ………………6分
即(81-d2)k2-54k+9-d2=0. ………………8分
∵k∈R,且d≠9,d>0,
∴Δ=(-54)2-4(81-d2)(9-d2)≥0,即0<d≤3且d≠9.………………12分
综合①②可知,所求d的变化范围为(0,3].

方法二:如图所示,显然有0<d≤|AB|.
而|AB|==3.
故所求的d的变化范围为(0,3].
(2)由图可知,当d取最大值时,两直线垂直于AB.
而kAB==,
∴所求直线的斜率为-3. 故所求的直线方程分别为
y-2=-3(x-6),y+1=-3(x+3),即3x+y-20=0和3x+y+10=0.
 .所以d的变化范围为
.所以d的变化范围为 .
.(2)由于当d最大时,AB与直线垂直,所以可以利用AB的斜率求出直线的斜率,进而求出其直线方程.
(1)方法一:①当两条直线的斜率不存在时,即两直线分别为x=6和x=-3,则它们之间的距离为9. ………………2分
②当两条直线的斜率存在时,设这两条直线方程为
l1:y-2=k(x-6),l2:y+1=k(x+3),
即l1:kx-y-6k+2=0,l2:kx-y+3k-1=0, ………………4分
∴d==. ………………6分
即(81-d2)k2-54k+9-d2=0. ………………8分
∵k∈R,且d≠9,d>0,
∴Δ=(-54)2-4(81-d2)(9-d2)≥0,即0<d≤3且d≠9.………………12分
综合①②可知,所求d的变化范围为(0,3].

方法二:如图所示,显然有0<d≤|AB|.
而|AB|==3.
故所求的d的变化范围为(0,3].
(2)由图可知,当d取最大值时,两直线垂直于AB.
而kAB==,
∴所求直线的斜率为-3. 故所求的直线方程分别为
y-2=-3(x-6),y+1=-3(x+3),即3x+y-20=0和3x+y+10=0.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
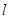 过点
过点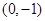 ,且与直线
,且与直线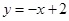 垂直,则直线
垂直,则直线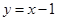
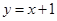
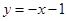
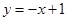
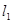 为曲线
为曲线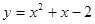 在点
在点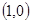 处的切线,
处的切线,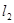 为该曲线的另一条切线,且
为该曲线的另一条切线,且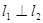 .
.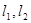 和
和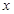 轴所围成的三角形的面积.
轴所围成的三角形的面积. 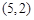 且在y轴上的截距是在x轴上的截距的2倍的直线方程是 .
且在y轴上的截距是在x轴上的截距的2倍的直线方程是 .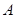
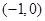 ,
,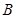
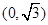 ,
,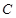
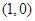 ,
,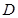
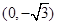 ,若动点M与点
,若动点M与点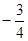 ,则
,则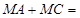 .
.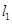 :
: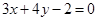 与
与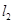 :
: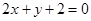 的交点
的交点 ,且垂直于直线
,且垂直于直线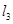 :
: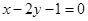 直线
直线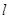 的方程.
的方程.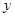 轴上的截距为
轴上的截距为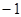 的直线方程是 ( )
的直线方程是 ( )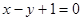
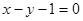
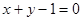
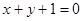
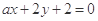 与直线
与直线 平行,那么系数
平行,那么系数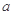 等于( )
等于( )