题目内容
(12分)(2011•福建)已知等差数列{an}中,a1=1,a3=﹣3.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{an}的前k项和Sk=﹣35,求k的值.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{an}的前k项和Sk=﹣35,求k的值.
(Ⅰ)an=1+(n﹣1)×(﹣2)=3﹣2n(Ⅱ)k=7
试题分析:(I)设出等差数列的公差为d,然后根据首项为1和第3项等于﹣3,利用等差数列的通项公式即可得到关于d的方程,求出方程的解即可得到公差d的值,根据首项和公差写出数列的通项公式即可;
(II)根据等差数列的通项公式,由首项和公差表示出等差数列的前k项和的公式,当其等于﹣35得到关于k的方程,求出方程的解即可得到k的值,根据k为正整数得到满足题意的k的值.
解:(I)设等差数列{an}的公差为d,则an=a1+(n﹣1)d
由a1=1,a3=﹣3,可得1+2d=﹣3,解得d=﹣2,
从而,an=1+(n﹣1)×(﹣2)=3﹣2n;
(II)由(I)可知an=3﹣2n,
所以Sn=
 =2n﹣n2,
=2n﹣n2,进而由Sk=﹣35,可得2k﹣k2=﹣35,
即k2﹣2k﹣35=0,解得k=7或k=﹣5,
又k∈N+,故k=7为所求.
点评:此题考查学生灵活运用等差数列的通项公式及前n项和的公式化简求值,是一道基础题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 (其中
(其中 ),区间
),区间 .
. 的长度(注:区间
的长度(注:区间 的长度定义为
的长度定义为 );
);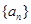 ,令
,令 ,证明:
,证明: .
. 同时满足:(1)各项均为正数,(2)存在常数k, 对任意
同时满足:(1)各项均为正数,(2)存在常数k, 对任意 都成立,那么,这样的数列
都成立,那么,这样的数列 , a2、a4、a5成等差数列,求的值;
, a2、a4、a5成等差数列,求的值; 对任意
对任意 都成立?若存在,求出λ;若不存在,说明理由.
都成立?若存在,求出λ;若不存在,说明理由. 的前
的前 项和为
项和为 ,向量
,向量 ,(
,(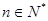 )满足
)满足 .
. 的通项公式为
的通项公式为 (
( ),若
),若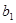 ,
, ,
, (
( )成等差数列,求
)成等差数列,求 和
和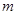 的值;
的值; 满足
满足 ,公比
,公比 满足
满足 ,且对任意正整数
,且对任意正整数 ,
, 仍是该数列中的某一项,求公比
仍是该数列中的某一项,求公比 中,
中, ,那么
,那么 ( )
( )