Question

【题目】已知在平面直角坐标系中，椭圆C：离心率为，其短轴长为2．

（1）求椭圆C的标准方程；

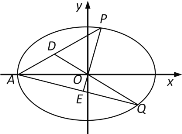
（2）如图，A为椭圆C的左顶点，P，Q为椭圆C上两动点，直线PO交AQ于E，直线QO交AP于D，直线OP与直线OQ的斜率分别为，，且， ，（为非零实数），求的值．

Answer 1

【答案】（1）（2）

【解析】

（1）由题意，求得，由，得，再利用，即可求得，得到椭圆的标准方程；

（2）由（1），设，因为，得到，

两边同时乘以得，，得到，，代入椭圆的方程得，同理得，即可得到结论.

（1）解：因为短轴长2b=2，所以b=1，

又离心率，所以，

所以，所以，

所以椭圆C的标准方程为．

（2）由（1），点A，设，

则

因为，所以，

由①得，， 由②得，，

所以，

两边同时乘以k1得，，

所以，，

代入椭圆的方程得，，

同理可得，，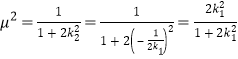

所以．