题目内容
已知函数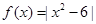 ,若
,若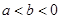 ,且
,且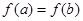 ,则
,则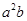 的最小值是( )
的最小值是( )
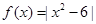 ,若
,若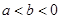 ,且
,且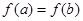 ,则
,则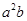 的最小值是( )
的最小值是( )| A.-16 | B.-12 | C.-10 | D.-8 |
A
试题分析:作出函数
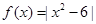 ,可知图中
,可知图中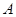 点坐标为
点坐标为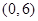 ,图中
,图中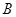 点坐标为
点坐标为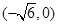 .令
.令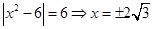 或
或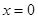 .即图中
.即图中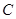 点坐标为
点坐标为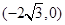 .由
.由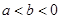 ,且
,且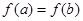 可知,
可知,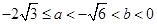 .由
.由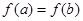 得
得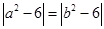 ,即
,即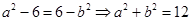 .
.所以
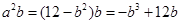 .令
.令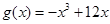 ,则
,则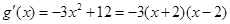 .所以当
.所以当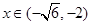 时,
时,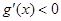 ;当
;当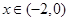 时,
时,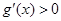 .即
.即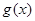 在
在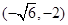 上单调递减,在
上单调递减,在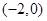 上单调递增.所以
上单调递增.所以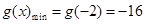 ,即当
,即当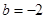 ,
,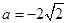 时,
时,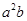 有最小值-16.
有最小值-16.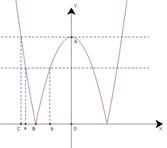

练习册系列答案
相关题目
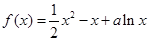 (其中
(其中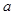 为常数).
为常数).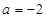 时,求函数
时,求函数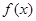 的最值;
的最值;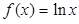 .
.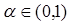 ,求
,求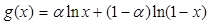 最大值;
最大值;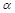 ,
,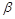 满足
满足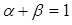 .求证:
.求证: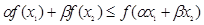 ;
;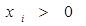 ,正数
,正数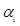 满足
满足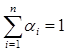 .证明:
.证明: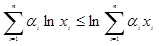
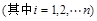 .
.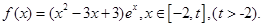
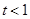 时,求函数
时,求函数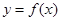 的单调区间;
的单调区间;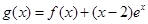 ,试问函数
,试问函数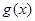 在
在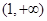 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.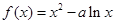 和
和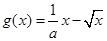 ,且
,且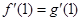 .
.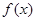 ,
,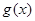 的表达式;
的表达式;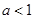 时,不等式
时,不等式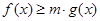 在
在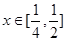 上恒成立,求实数
上恒成立,求实数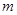 的取值范围.
的取值范围.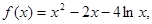 则f′(x)
则f′(x)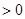 的解集为( )
的解集为( )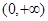
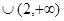
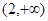
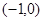
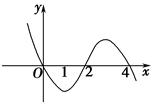
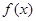 ,对任意x都有
,对任意x都有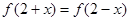 ,且其导函数
,且其导函数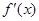 满足
满足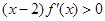 ,则当
,则当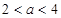 时,有( )
时,有( )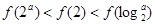
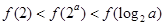
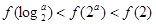
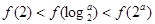
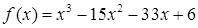 的单调减区间为 .
的单调减区间为 .