已知x.y为正实数.则( )A．2lgx+lgy=2lgx+2lgyB．2lg(x+y)=2lgx•2lgyC．2lgx•lgy=2lgx+2lgyD．2lg(xy)=2lgx•2lgy 题目和参考答案——青夏教育精英家教网——

题目内容

（2013•浙江）已知x，y为正实数，则（　　）

A．2^lgx+lgy=2^lgx+2^lgy	B．2^lg^（x+y）=2^lgx•2^lgy
C．2^lgx•lgy=2^lgx+2^lgy	D．2^lg^（xy）=2^lgx•2^lgy

D

因为a^s+t=a^s•a^t，lg（xy）=lgx+lgy（x，y为正实数），
所以2^lg^（xy）=2^lgx+lgy=2^lgx•2^lgy，满足上述两个公式，
故选D．

练习册系列答案

初中同步导学与测试系列答案

金手指同步练测卷系列答案

中考全接触系列答案

中考说明与训练系列答案

中考备考每天一点系列答案

征服英语名师课时计划系列答案

考前系列答案

口算心算快速算系列答案

跨越中考总复习方略系列答案

新语文阅读训练系列答案

相关题目

设a＝log₃6，b＝log₅10，c＝log₇14，则a，b，c的大小关系为________．

幂指函数y＝f(x)^g(x)在求导数时，可以运用对数法：在函数解析式两边求对数得

，两边求导数得

，于是y′＝f(x)^g(x)·

．运用此法可以探求得知y＝

的一个单调递增区间为(　　)．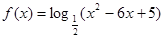

的单调递减区间是．

函数f（x）=㏑x的图象与函数g（x）=x²﹣4x+4的图象的交点个数为（　　）

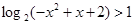的解集为( )

设a＞1，若对任意的x∈[a，2a]，都有y∈[a，a²]满足方程log_ax＋log_ay＝3，则a的取值范围是________．