题目内容
(12分)已知函数
(1)判断函数的奇偶性和单调性;
(2)当 时,有
时,有 ,求
,求 的取值范围.
的取值范围.
【答案】
解:(1)奇函数.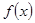 增函数.(2)
增函数.(2)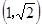 .
.
【解析】本题主要考查了证明函数奇偶性的方法,利用函数单调性的定义证明函数单调性的方法步骤,代数变形能力和逻辑推理能力。
(1)先确定函数的定义域,再利用奇函数的定义,证明函数f(x)=-f(-x),从而函数为奇函数;
(2)因为 所以
所以 即
即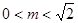 ,由(1)得
,由(1)得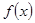 为奇函数且是R上的增函数,进而解得。
为奇函数且是R上的增函数,进而解得。
解:(1)函数的定义域为R ,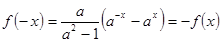 所以
所以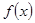 为奇函数.
为奇函数.
当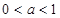 时
时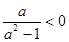 ,
,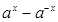 单调递减所以
单调递减所以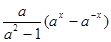 单调递增;
单调递增;
当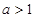 时
时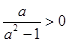 ,
,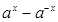 单调递增所以
单调递增所以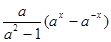 单调递增.
单调递增.
总上所述函数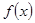 增函数.
增函数.
(2)因为 所以
所以 即
即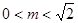 ,由(1)得
,由(1)得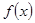 为奇函数且是R上的增函数所以由
为奇函数且是R上的增函数所以由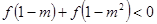 得
得 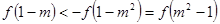
即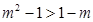
解得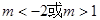 综上得
综上得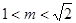 所以
所以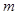 的取值范围是
的取值范围是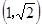 .
.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
 的定义域为集合A,
的定义域为集合A,  的值域为集合B.
的值域为集合B. ,求
,求 ;
; ,求实数
,求实数 的取值范围。
的取值范围。 的导函数
的导函数 ,数列
,数列 的前
的前 项和为
项和为 ,点
,点 均在函数
均在函数 的图象上.
的图象上.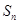 的最大值;
的最大值; ,其中
,其中 ,求
,求 的前
的前 是偶函数.
是偶函数. 有解,求m的取值范围.
有解,求m的取值范围.