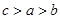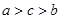题目内容
某种海洋生物的身长f(t)(单位:米)与生长年限t(单位:年)满足如下的函数关系:
f(t)=
.(设该生物出生时的时刻t=0)
(1)需经过多少时间,该生物的身长超过8米?
(2)该生物出生后第3年和第4年各长了多少米?并据此判断,这2年中哪一年长得更快.
f(t)=
| 10 |
| 1+2-t+4 |
(1)需经过多少时间,该生物的身长超过8米?
(2)该生物出生后第3年和第4年各长了多少米?并据此判断,这2年中哪一年长得更快.
(1)设f(t)=
≥8,
即2-t+4≤
,
解得t≥6,
即该生物6年后身长可超过8米.
(2)由于f(3)-f(2)=
-
=
,
f(4)-f(3)=
-
=
,
∴第3年长了
米,第4年长了
米,
∴
>
,
∴第4年长得快.
| 10 |
| 1+2-t+4 |
即2-t+4≤
| 1 |
| 4 |
解得t≥6,
即该生物6年后身长可超过8米.
(2)由于f(3)-f(2)=
| 10 |
| 1+2 |
| 10 |
| 1+22 |
| 4 |
| 3 |
f(4)-f(3)=
| 10 |
| 1+1 |
| 10 |
| 1+2 |
| 5 |
| 3 |
∴第3年长了
| 4 |
| 3 |
| 5 |
| 3 |
∴
| 5 |
| 3 |
| 4 |
| 3 |
∴第4年长得快.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
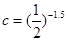 ,则( ).
,则( ). ,则下列不等式成立的是( )
,则下列不等式成立的是( )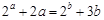 ,则
,则

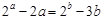 ,则
,则 则( )
则( )



 ,
, ,
, ,则( )
,则( )