题目内容
3.等比数列{an}中,an>0,公比q=$\sqrt{2}$,a4•a8=8,则a2•a6•a7=( )| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
分析 由已知得a6=2$\sqrt{2}$,从而得到a1=$\frac{1}{2}$,由此能求出a2•a6•a7的值.
解答 解:∵等比数列{an}中,an>0,公比q=$\sqrt{2}$,
a4•a8=${{a}_{6}}^{2}$=8,
∴a6=2$\sqrt{2}$,
∴${a}_{1}•(\sqrt{2})^{5}$=2$\sqrt{2}$,解得a1=$\frac{2\sqrt{2}}{(\sqrt{2})^{5}}$=$\frac{1}{2}$,
∴a2•a6•a7=2$\sqrt{2}$•a2a7
=2$\sqrt{2}$×($\frac{1}{2}×\sqrt{2}$)×[$\frac{1}{2}×(\sqrt{2})^{6}$]
=8.
故选:C.
点评 本题考查等比数列的三项乘积的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
相关题目
11.设非零向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,则θ∈($\frac{π}{2}$,π)是$\overrightarrow{a}$•$\overrightarrow{b}$<0的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
18.如图,在复平面内,复数z1和z2对应的点分别是A和B,则$\frac{{z}_{2}}{{z}_{1}}$=( )
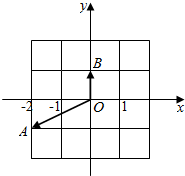

| A. | $\frac{1}{5}$+$\frac{2}{5}$i | B. | $\frac{2}{5}$+$\frac{1}{5}$i | C. | -$\frac{1}{5}$-$\frac{2}{5}$i | D. | -$\frac{2}{5}$-$\frac{1}{5}$i |
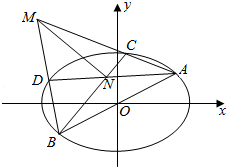 如图,在平面直角坐标系xoy中,椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,直线l:y=$\frac{1}{2}$x与椭圆E相交于A,B两点,AB=$4\sqrt{5}$,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N.
如图,在平面直角坐标系xoy中,椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,直线l:y=$\frac{1}{2}$x与椭圆E相交于A,B两点,AB=$4\sqrt{5}$,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N.