题目内容
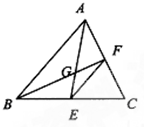 (几何证明选讲选做题)已知G是△ABC的重心,AG交BC于E,BG交AC于F,△EFG的面积为1,则△EFC的面积为
(几何证明选讲选做题)已知G是△ABC的重心,AG交BC于E,BG交AC于F,△EFG的面积为1,则△EFC的面积为分析:本题考查三角形的重心性质,重心的几何特征到顶点的距离到到对边中点距离的2倍,由此比例关系求△EFC的面积,即可得到正确答案.
解答:解:因为G为三角形的重心 那么AF AE 分别为BC AC的中线
那么 EF平行与AB 所以△GBA和△GEF为相似三角形
所以
=(
)2=
则 S△GBA=4
又因为
=
,S△GBA=4
S△AGE=2
同理 S△BGF=2
所以四边型EFAB面积为9
设 S△CEF=x,则
=
S△CEF=3
故答案为3
那么 EF平行与AB 所以△GBA和△GEF为相似三角形
所以
| S△GEF |
| S△GBA |
| 1 |
| 2 |
| 1 |
| 4 |
则 S△GBA=4
又因为
| GE |
| BG |
| 1 |
| 2 |
S△AGE=2
同理 S△BGF=2
所以四边型EFAB面积为9
设 S△CEF=x,则
| x |
| x+9 |
| 1 |
| 4 |
S△CEF=3
故答案为3
点评:本题考查三角形的五心,三角形的五心是三角形的重要性质,本题考查重心的几何性质,理解重心的几何性质是解本题的关键

练习册系列答案
相关题目
 (几何证明选讲选做题)
(几何证明选讲选做题) (几何证明选讲选做题)如图,四边形ABCD内接于⊙O,AB为⊙O的直径,直线MN切⊙O于D,∠MDA=60°,则∠BCD=
(几何证明选讲选做题)如图,四边形ABCD内接于⊙O,AB为⊙O的直径,直线MN切⊙O于D,∠MDA=60°,则∠BCD= (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (几何证明选讲选做题)
(几何证明选讲选做题)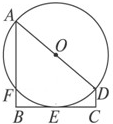 (几何证明选讲选做题)
(几何证明选讲选做题)