6人站成一排.甲不站左端.乙不站右端.用多少种不同的站法? 题目和参考答案——青夏教育精英家教网——

题目内容

17．6人站成一排，甲不站左端，乙不站右端，用多少种不同的站法？（用直接法）

分析甲不站排头，乙不站排尾，可按甲在尾与不在尾分为两类直接求解即可；

解答解：甲不站排头，乙不站排尾排法计数可分为两类，第一类甲在右端，排法和数有A₅⁵，第二类甲不在右端，先排甲，有A₄¹种方法，再排乙有A₄¹种方法，剩下的四人有A₄⁴种排法，故有A₄¹×A₄¹×A₄⁴种方法，由此，总排法有A₅⁵+A₄¹×A₄¹×A₄⁴=504；
故答案为：504．

点评本题考查排列、组合及简单计数问题，做题时要注意体会这些方法的原理及其实际意义．注意分类讨论此处容易遗漏出错，做题时切记．

练习册系列答案

导学先锋系列答案

零负担试卷系列答案

名牌学校分层周周测系列答案

53金卷3年高考模拟试卷整编系列答案

黄冈海淀全程培优测试卷系列答案

高中同步检测优化卷阶梯训练系列答案

高中同步阶梯训练示范卷系列答案

成功阶梯步步高系列答案

同步学习与辅导系列答案

超能学典各地期末试卷精选系列答案

相关题目

7．若直线l：ax-by=1与不等式组$\left\{\begin{array}{l}y＜1\\ 3x-y-2＜0\\ 3x+y+2＞0\end{array}\right.$表示的平面区域无公共点，则3a-2b的最小值为（　　）

$-\frac{11}{2}$

8．已知集合A={-1，i}，i为虚数单位，则下列选项正确的是（　　）

$\frac{1}{i}$∈A

$\frac{1-i}{1+i}$∈A

5．若函数f（x）=sinxcosx+a（sinx+cosx）的定义域为[0，$\frac{π}{2}$]，若a≥-1，且函数f（x）的最大值比最小值大$\frac{\sqrt{2}}{2}$，求a的值．

12．已知D=$\left\{\begin{array}{l}{2x-y+k≥0}\\{x+y≥0}\\{x≤2}\end{array}\right.$，?m（x，y）∈D恒有2x-5y+10k+15＞0，?N（x₀，y₀）∈D使得-7x₀+2y₀-5k²+2＞0，则k∈$\frac{1}{5}$＜k＜1．

2．比较y₁=4^0.9，y₂=8^0.48，y₃=（$\frac{1}{2}$）^-1.5大小．

9．两条平行的直线分别经过点A（3，0），B（0，4），它们之间的距离d满足的条件是（　　）

14．某流程图如图所示，现输入如下四个函数，则可以输出f（x）的是（　　）

f（x）=-x²+1

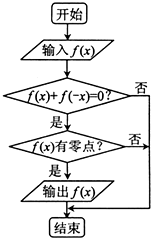
f（x）=x+$\frac{1}{x}$

f（x）=lg$\frac{1+x}{1-x}$

f（x）=$\frac{{2}^{x}+1}{{2}^{x}-1}$

15．已知过点A（1，m）恰能作曲线f（x）=x³-3x的两条切线，则m的值是（　　）