题目内容
1.如图所示,圆O为正三角形ABC的内切圆,P为圆O上一点,向量$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x+y的取值范围为( )
| A. | [$\frac{1}{2}$,1] | B. | [$\frac{1}{3}$,1] | C. | [$\frac{1}{4}$,1] | D. | [$\frac{1}{3}$,$\frac{1}{2}$] |
分析 如图所示,建立直角坐标系,不妨设AC=2.A(-1,0),B(0,$\sqrt{3}$),C(1,0).则内切圆O的半径r=OD=$\frac{\sqrt{3}}{3}$.可得内切圆的标准方程为:${x}^{2}+(y-\frac{\sqrt{3}}{3})^{2}$=$\frac{1}{3}$.设P的坐标$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{3}cosθ}\\{y=\frac{\sqrt{3}}{3}+\frac{\sqrt{3}}{3}sinθ}\end{array}\right.$,θ∈[0,2π).由于向量$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,可得x+2y=$\frac{\sqrt{3}}{3}cosθ$+1,$\sqrt{3}$x=$\frac{\sqrt{3}}{3}+\frac{\sqrt{3}}{3}sinθ$.化简即可得出.
解答 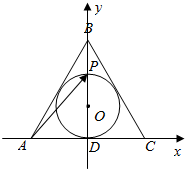 解:如图所示,建立直角坐标系,
解:如图所示,建立直角坐标系,
不妨设AC=2.A(-1,0),B(0,$\sqrt{3}$),C(1,0).
则内切圆O的半径r=OD=AD•tan30°=$\frac{\sqrt{3}}{3}$.
可得内切圆的标准方程为:${x}^{2}+(y-\frac{\sqrt{3}}{3})^{2}$=$\frac{1}{3}$.
设P的坐标$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{3}cosθ}\\{y=\frac{\sqrt{3}}{3}+\frac{\sqrt{3}}{3}sinθ}\end{array}\right.$,θ∈[0,2π).
∵向量$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,
∴$(\frac{\sqrt{3}}{3}cosθ+1,\frac{\sqrt{3}}{3}+\frac{\sqrt{3}}{3}sinθ)$=x(1,$\sqrt{3}$)+y(2,0),
∴x+2y=$\frac{\sqrt{3}}{3}cosθ$+1,$\sqrt{3}$x=$\frac{\sqrt{3}}{3}+\frac{\sqrt{3}}{3}sinθ$.
∴x+y=$\frac{\sqrt{3}}{6}cosθ+\frac{1}{6}sinθ$+$\frac{2}{3}$
=$\frac{1}{3}sin(θ+\frac{π}{3})$+$\frac{2}{3}$∈$[\frac{1}{3},1]$.
故选:B.
点评 本题考查了圆的标准方程、正三角形的性质、向量线性运算、和差公式,考查了推理能力与计算能力,属于中档题.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案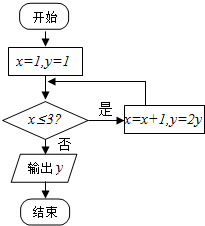
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |