题目内容
若x为实数，[x]表示不超过x的最大整数，例如[2.3]=2，[-1.2]=-2．记{x}=x-[x]．设a=
，b=[
]，c={
}，求b，c的值．判断实数a、b、c是否成等差数列或等比数列，并说明理由．
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
分析：确定b，c的值，利用等比数列的定义，即可得到结论．
解答：解：∵1＜
＜2，∴b=[
]=1
依题意c={
}=a-b=
-1=
∵
×
=1
∴ac=b2，
所以a、b、c成等比数列．
| ||
| 2 |
| ||
| 2 |
依题意c={
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∵
| ||
| 2 |
| ||
| 2 |
∴ac=b2，
所以a、b、c成等比数列．
点评：本题考查新定义，考查等比数列的定义，解题的关键是理解新定义，属于基础题．
练习册系列答案
怎样学好牛津英语系列答案
导学教程高中新课标系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）+B（A＞0，ω＞0）的一系列对应值如下表：
（1）根据表格提供的数据求函数f（x）的一个解析式．
（2）根据（1）的结果，若函数y=f（kx）（k＞0）周期为
，当x∈[0，
]时，方程f（kx）=m恰有两个不同的解，求实数m的取值范围．
| x | -
|
|
|
|
|
|
| ||||||||||||||
| y | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
（2）根据（1）的结果，若函数y=f（kx）（k＞0）周期为
| 2π |
| 3 |
| π |
| 3 |
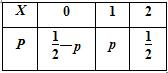若p为非负实数，随机变量X的概率分布如表，则E（X）的最大值为
已知函数f（x）的定义域为[-2，+∞），部分对应值如下表．f′（x）为f（x）的导函数，函数y=f′（x）的图象如图所示．若实数a满足f（2a+1）＜1，则a的取值范围是（ ）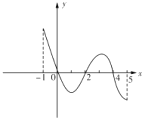
（2013•湖南模拟）已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f′（x）的图象如图所示．