题目内容
(本题满分14分)
已知如图,椭圆方程为![]()
![]() .P为椭圆上的动点,
.P为椭圆上的动点,
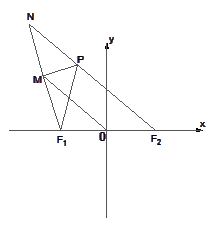
F1、F2为椭圆的两焦点,当点P不在x轴上时,过F1作∠F1PF2的外角
平分线的垂线F1M,垂足为M,当点P在x轴上时,定义M与P重合.
(1)求M点的轨迹T的方程;
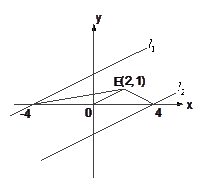
(2)已知![]() 、
、![]() ,试探究是否存在这样的点
,试探究是否存在这样的点![]() :
:![]() 是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积
是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积![]() ?若存在,求出点Q的坐标,若不存在,说明理由.
?若存在,求出点Q的坐标,若不存在,说明理由.
![]() ,
,![]()
![]() .
.
解析:
解:(1)当点P不在x轴上时,延长F1M与F2P的延长线相交于点N,连结OM,
∵![]() ,
,![]() ∴
∴![]() ≌
≌![]() ∴M是线段
∴M是线段![]() 的中点,
的中点,
![]() |----------------------------------------------------2分
|----------------------------------------------------2分
∴ ![]() =
=![]()
![]() =
=![]() =
=![]()
∵点P在椭圆上
∴![]() =
=![]() ∴
∴![]() =4,----------------------4分
=4,----------------------4分
当点P在x轴上时,M与P重合
 ∴M点的轨迹T的方程为:
∴M点的轨迹T的方程为:![]() .----------------------6分
.----------------------6分
(2)连结OE,易知轨迹T上有两个点
A![]() ,B
,B![]() 满足
满足![]() ,
,
分别过A、B作直线OE的两条平行线![]() 、
、![]() .
.
∵同底等高的两个三角形的面积相等
∴符合条件的点均在直线![]() 、
、![]() 上.------------------------------------7分
上.------------------------------------7分
∵![]() ∴直线
∴直线![]() 、
、![]() 的方程分别为:
的方程分别为:![]() 、
、![]() -------------------8分
-------------------8分
设点![]() (
(![]() )∵
)∵![]() 在轨迹T内,∴
在轨迹T内,∴![]() -------------------------9分
-------------------------9分
分别解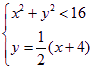 与
与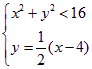
得![]() 与
与![]() -------------------------------------------------11分
-------------------------------------------------11分
∵![]() ∴
∴![]() 为偶数,在
为偶数,在![]() 上
上![]() 对应的
对应的![]()
在![]() 上
上![]() ,对应的
,对应的![]() --------------------------------------13分
--------------------------------------13分
∴满足条件的点![]() 存在,共有6个,它们的坐标分别为:
存在,共有6个,它们的坐标分别为:
![]()
![]() .-----------------------------14分
.-----------------------------14分

 B=[0,3],求实数m的值
B=[0,3],求实数m的值 CRB,求实数m的取值范围
CRB,求实数m的取值范围 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。 ,在动点
,在动点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。 .
. 的定义域;
的定义域; 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使
 ).
).