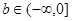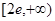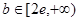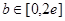题目内容
已知函数 (
(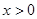 ,
,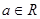 ),
),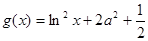 .
.
(Ⅰ)证明:当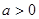 时,对于任意不相等的两个正实数
时,对于任意不相等的两个正实数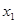 、
、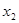 ,均有
,均有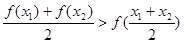 成立;
成立;
(Ⅱ)记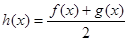 ,
,
(ⅰ)若 在
在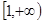 上单调递增,求实数
上单调递增,求实数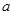 的取值范围;
的取值范围;
(ⅱ)证明: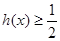 .
.
 (
(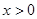 ,
,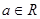 ),
),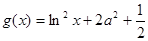 .
.(Ⅰ)证明:当
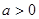 时,对于任意不相等的两个正实数
时,对于任意不相等的两个正实数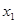 、
、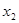 ,均有
,均有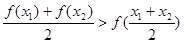 成立;
成立;(Ⅱ)记
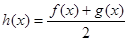 ,
,(ⅰ)若
 在
在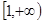 上单调递增,求实数
上单调递增,求实数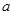 的取值范围;
的取值范围;(ⅱ)证明:
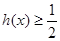 .
.(Ⅰ)详见解析;(Ⅱ)(ⅰ)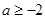 ,(ⅱ) 详见解析.
,(ⅱ) 详见解析.
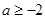 ,(ⅱ) 详见解析.
,(ⅱ) 详见解析.试题分析:(Ⅰ)当
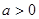 时,对于任意不相等的两个正实数
时,对于任意不相等的两个正实数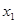 、
、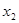 ,均有
,均有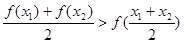 成立,只需求出
成立,只需求出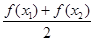 与
与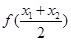 的解析式,两式作差得
的解析式,两式作差得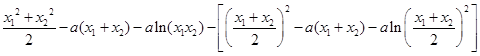
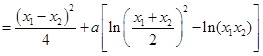 ,判断符号即可证明;(Ⅱ)记
,判断符号即可证明;(Ⅱ)记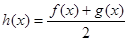 ,若
,若 在
在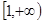 上单调递增,求实数
上单调递增,求实数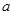 的取值范围,首先求出
的取值范围,首先求出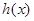 的解析式,从而得
的解析式,从而得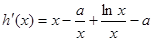 ,若它在
,若它在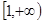 上单调递增,即它的导函数在
上单调递增,即它的导函数在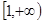 上恒大于零,得
上恒大于零,得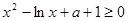 恒成立,这是恒成立问题,只需把含有
恒成立,这是恒成立问题,只需把含有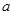 的放到不等式的一侧,不含
的放到不等式的一侧,不含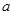 的放到不等式的另一侧,即
的放到不等式的另一侧,即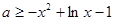 ,转化为求
,转化为求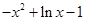 的最大值问题,可利用导数求出最大值,从而可得实数
的最大值问题,可利用导数求出最大值,从而可得实数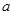 的取值范围. 证明:
的取值范围. 证明: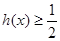 ,因为
,因为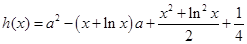 ,只需证它的最小值为
,只需证它的最小值为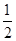 ,可利用导数证明它的最小值为
,可利用导数证明它的最小值为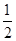 即可.
即可.试题解析:(Ⅰ)证明:
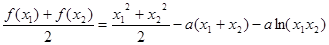 ,
,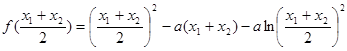 ,
,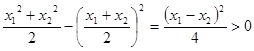 ,则
,则 ①
①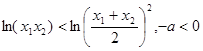 ,则
,则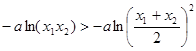 ,②
,②由①②知
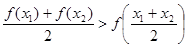 .
.(Ⅱ)(ⅰ)
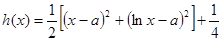 ,
,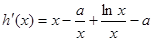 ,
,令
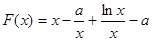 ,则
,则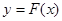 在
在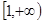 上单调递增.
上单调递增.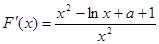 ,则当
,则当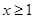 时,
时,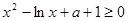 恒成立,
恒成立,即当
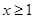 时,
时,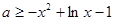 恒成立.
恒成立. 令
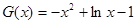 ,则当
,则当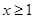 时,
时,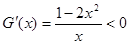 ,
,故
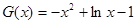 在
在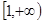 上单调递减,从而
上单调递减,从而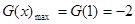 ,
,故
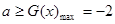 .(14分)
.(14分)(ⅱ)法一:
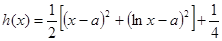 ,令
,令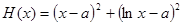 ,
,则
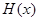 表示
表示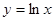 上一点
上一点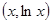 与直线
与直线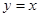 上一点
上一点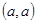 距离的平方.
距离的平方.令
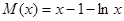 ,则
,则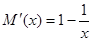 ,
,可得
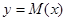 在
在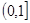 上单调递减,在
上单调递减,在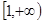 上单调递增,
上单调递增,故
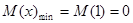 ,则
,则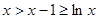 ,
,直线
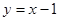 与
与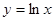 的图象相切与点
的图象相切与点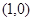 ,点
,点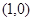 到直线
到直线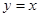 的距离为
的距离为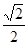 ,
,则
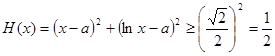 ,故
,故 .
.法二:
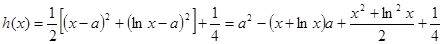 ,
,令
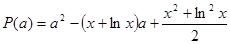 ,则
,则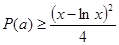 .
.令
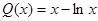 ,则
,则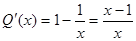 ,显然
,显然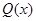 在
在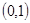 上单调递减,在
上单调递减,在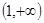 上单调递增,
上单调递增,则
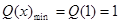 ,则
,则 ,故
,故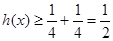 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 )为函数
)为函数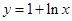 图像上一点,O为坐标原点,记直线OP的斜率
图像上一点,O为坐标原点,记直线OP的斜率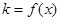 。
。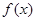 的单调区间;
的单调区间;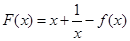 ,求函数
,求函数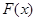 的最小值。
的最小值。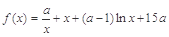 ,
,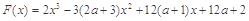 ,其中
,其中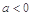 且
且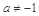 .
. 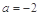 ,求函数
,求函数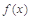 的单调递增区间;
的单调递增区间;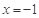 时,函数
时,函数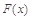 有极值,求函数
有极值,求函数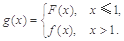 (
(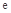 是自然对数的底数),是否存在a使
是自然对数的底数),是否存在a使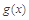 在
在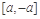 上为减函数,若存在,求实数a的范围;若不存在,请说明理由.
上为减函数,若存在,求实数a的范围;若不存在,请说明理由.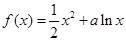 .
.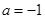 ,求函数
,求函数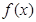 的极值,并指出是极大值还是极小值;
的极值,并指出是极大值还是极小值;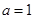 ,求证:在区间
,求证:在区间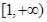 上,函数
上,函数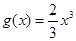 的图像的下方.
的图像的下方.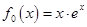 ,
,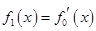 ,
,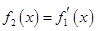 ,
,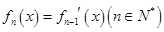 .
. 表达式(不需证明);
表达式(不需证明); ;
;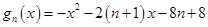 ,
,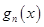 的最大值为
的最大值为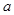 ,
,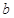 ,试求
,试求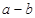 的最小值.
的最小值.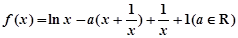 .
.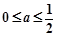 时,试讨论
时,试讨论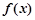 的单调性;
的单调性;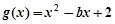 ,当
,当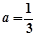 时,若对任意
时,若对任意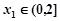 ,存在
,存在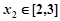 ,使
,使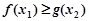 ,求实数
,求实数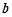 取值范围.
取值范围.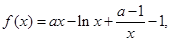 试讨论
试讨论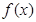 的单调性.
的单调性.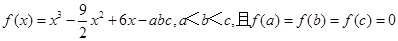 ,现给出如下结论:
,现给出如下结论: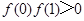 ;②
;②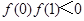 ;③
;③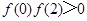 ;④
;④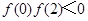 .
.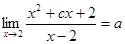 ,且函数
,且函数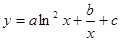 在
在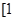 ,
,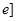 上存在反函数,则( )
上存在反函数,则( )