题目内容
已知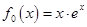 ,
,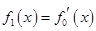 ,
,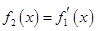 ,
,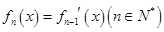 .
.
(Ⅰ)请写出的 表达式(不需证明);
表达式(不需证明);
(Ⅱ)求 的极小值
的极小值 ;
;
(Ⅲ)设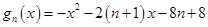 ,
,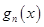 的最大值为
的最大值为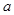 ,
, 的最小值为
的最小值为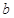 ,试求
,试求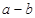 的最小值.
的最小值.
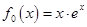 ,
,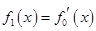 ,
,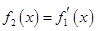 ,
,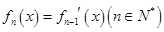 .
.(Ⅰ)请写出的
 表达式(不需证明);
表达式(不需证明);(Ⅱ)求
 的极小值
的极小值 ;
;(Ⅲ)设
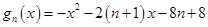 ,
,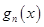 的最大值为
的最大值为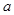 ,
, 的最小值为
的最小值为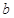 ,试求
,试求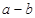 的最小值.
的最小值.(Ⅰ) ;(Ⅱ)
;(Ⅱ) 的极小值
的极小值 ;(Ⅲ)
;(Ⅲ)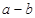 的最小值为
的最小值为 .
.
 ;(Ⅱ)
;(Ⅱ) 的极小值
的极小值 ;(Ⅲ)
;(Ⅲ)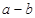 的最小值为
的最小值为 .
.试题分析:(Ⅰ)先由已知条件写出
 ,
, 的表达式,观察式子的结构特征,用不完全归纳法归纳出
的表达式,观察式子的结构特征,用不完全归纳法归纳出 表达式(可以用数学归纳法给出证明);(Ⅱ)由(Ⅰ)知
表达式(可以用数学归纳法给出证明);(Ⅱ)由(Ⅰ)知 的表达式,要求极值点,就要借助
的表达式,要求极值点,就要借助 的导函数
的导函数 ,令
,令 ,解出可能的极值点,验证是极值后代入解析式,即可求出
,解出可能的极值点,验证是极值后代入解析式,即可求出 的最小值
的最小值 ;(Ⅲ)类比求函数
;(Ⅲ)类比求函数 的最小值的过程,即可求出函数
的最小值的过程,即可求出函数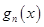 的极大值
的极大值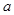 ,进而求出函数
,进而求出函数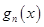 的最大值,从而得
的最大值,从而得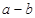 的关系式,将它看作数列,研究该数列相邻两项的关系,即可求得
的关系式,将它看作数列,研究该数列相邻两项的关系,即可求得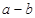 的最小值;得
的最小值;得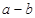 的关系式
的关系式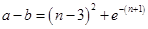 后,也可以构造函数
后,也可以构造函数 ,利用导数求它的最小值,即得
,利用导数求它的最小值,即得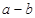 的最小值.
的最小值.试题解析:(Ⅰ)
 4分
4分(Ⅱ)∵
 ,∴当
,∴当 时,
时, ;当
;当 时,
时, ,∴当
,∴当 时,
时, 取得极小值
取得极小值 ,即
,即 (
( ) 8分
) 8分(Ⅲ)解法一:∵
 ,所以
,所以 . 9分
. 9分又
 ,∴
,∴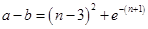 ,令
,令 ,则
,则 . 10分
. 10分∵
 在
在 单调递增,∴
单调递增,∴ ,∵
,∵ ,
, ,
,∴存在
 使得
使得 . 12分
. 12分∵
 在
在 单调递增,∴当
单调递增,∴当 时,
时, ;当
;当 时,
时, ,即
,即 在
在 单调递增,在
单调递增,在 单调递减,∴
单调递减,∴ ,又∵
,又∵ ,
, ,
, ,
,∴当
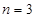 时,
时,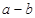 取得最小值
取得最小值 . 14分
. 14分解法二: ∵
 ,所以
,所以 . 9分
. 9分又
 ,∴
,∴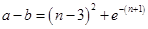 ,令
,令 ,则
,则 , 10分
, 10分当
 时,
时, ,又因为
,又因为 ,所以
,所以 ,
, ,
, ,
,∴
 ,所以
,所以 . 12分
. 12分又
 ,
, ,∴当
,∴当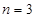 时,
时,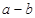 取得最小值
取得最小值 . 14分
. 14分
练习册系列答案
相关题目
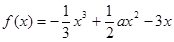 ,
,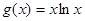
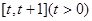 上的最小值;
上的最小值;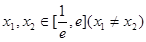 ,使方程
,使方程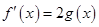
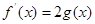 成立,求实数a的取值范围(其中e=2.71828是自然对数的底数)
成立,求实数a的取值范围(其中e=2.71828是自然对数的底数)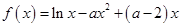 .
.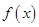 在
在 处取得极值,求实数
处取得极值,求实数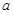 的值;
的值;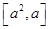 上的最大值.
上的最大值.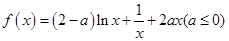 .
.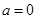 时,求
时,求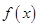 的极值;(2)当
的极值;(2)当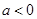 时,讨论
时,讨论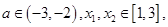 恒有
恒有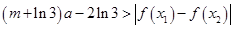 成立,求实数
成立,求实数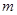 的取值范围.
的取值范围.  (
(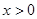 ,
,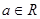 ),
),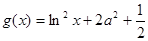 .
.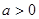 时,对于任意不相等的两个正实数
时,对于任意不相等的两个正实数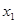 、
、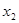 ,均有
,均有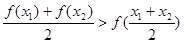 成立;
成立;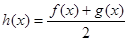 ,
, 在
在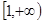 上单调递增,求实数
上单调递增,求实数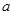 的取值范围;
的取值范围;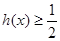 .
.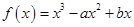 的图象与直线
的图象与直线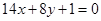 相切于点
相切于点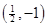 .
.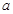 和
和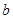 的值; (2)求
的值; (2)求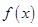 的极值.
的极值.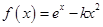 ,
, .
.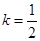 ,求证:当
,求证:当 时,
时,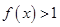 ;
;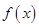 在区间
在区间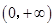 上单调递增,试求
上单调递增,试求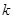 的取值范围;
的取值范围; .
.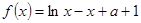
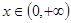 使得
使得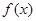 ≥0成立,求
≥0成立,求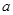 的范围
的范围 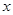 >1时,在(1)的条件下,
>1时,在(1)的条件下,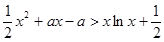 成立
成立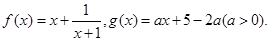
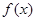 在
在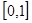 上的单调性,并用定义加以证明;
上的单调性,并用定义加以证明;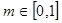 ,总存在
,总存在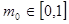 ,使得
,使得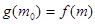 成立,求实数
成立,求实数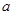 的取值范围
的取值范围