题目内容
已知函数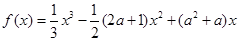 .
.
(1)若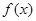 在
在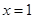 处取得极大值,求实数
处取得极大值,求实数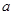 的值;
的值;
(2)若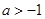 ,求
,求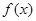 在区间
在区间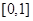 上的最大值.
上的最大值.
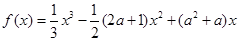 .
.(1)若
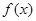 在
在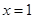 处取得极大值,求实数
处取得极大值,求实数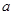 的值;
的值;(2)若
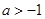 ,求
,求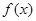 在区间
在区间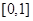 上的最大值.
上的最大值.(1)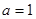 ;(2)详见解析.
;(2)详见解析.
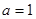 ;(2)详见解析.
;(2)详见解析.试题分析:(1) 本小题首先利用导数的公式和法则求得原函数的导函数,通过列表分析其单调性,进而寻找极大值点;(2) 本小题结合(1)中的分析可知参数
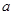 的取值范围影响函数在区间
的取值范围影响函数在区间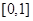 上的单调性,于是对参数
上的单调性,于是对参数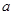 的取值范围进行分段讨论,从而求得函数在区间
的取值范围进行分段讨论,从而求得函数在区间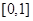 上的单调性,进而求得该区间上的最大值.
上的单调性,进而求得该区间上的最大值.试题解析:(1)因为
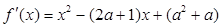
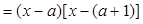
令
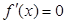 ,得
,得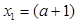 ,
,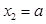
所以
 ,
, 随
随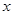 的变化情况如下表:
的变化情况如下表: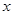 | 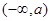 | 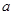 | 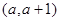 | 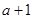 | 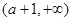 |
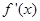 | 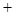 | 0 | 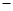 | 0 | 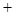 |
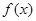 | ↗ | 极大值 | ↘ | 极小值 | ↗ |
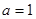 6分
6分(2)因为
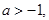 所以
所以 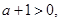
当
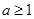 时,
时,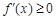 对
对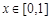 成立
成立所以当
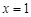 时,
时,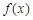 取得最大值
取得最大值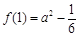
当
 时, 在
时, 在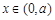 时,
时,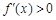 ,
,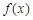 单调递增
单调递增在
 时,
时,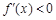 ,
,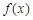 单调递减
单调递减所以当
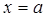 时,
时,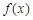 取得最大值
取得最大值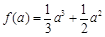
当
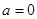 时, 在
时, 在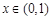 时,
时,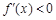 ,
,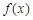 单调递减
单调递减所以当
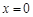 时,
时,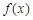 取得最大值
取得最大值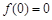
当
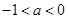 时,在
时,在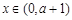 时,
时,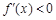 ,
,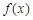 单调递减
单调递减在
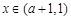 时,
时,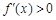 ,
,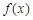 单调递增
单调递增又
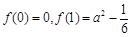 ,
,当
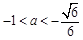 时,
时,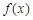 在
在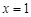 取得最大值
取得最大值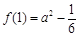
当
 时,
时,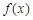 在
在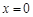 取得最大值
取得最大值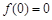
当
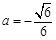 时,
时,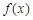 在
在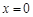 ,
,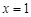 处都取得最大值0. 14分
处都取得最大值0. 14分综上所述,
当
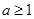 或
或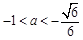 时,
时,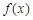 取得最大值
取得最大值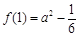
当
 时,
时,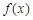 取得最大值
取得最大值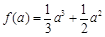
当
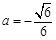 时,
时,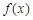 在
在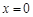 ,
,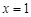 处都取得最大值0
处都取得最大值0当
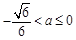 时,
时,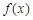 在
在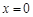 取得最大值
取得最大值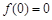 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
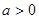 且函数
且函数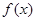 在区间
在区间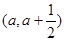 上存在极值,求实数
上存在极值,求实数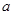 的取值范围;
的取值范围;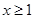 时,不等式
时,不等式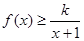 恒成立,求实数
恒成立,求实数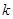 的取值范围.
的取值范围. +
+ ,g(x)=
,g(x)= ln(2ex)(其中e为自然对数的底数)
ln(2ex)(其中e为自然对数的底数) }中,a1=1,
}中,a1=1, )(n≥2),求证:
)(n≥2),求证: <
< <
< .
. .
. ,求
,求 的极值;
的极值; 的取值范围.
的取值范围.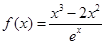 .
.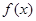 的极大值和极小值;
的极大值和极小值;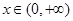 时,
时,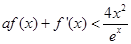 恒成立,求
恒成立,求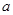 的取值范围.
的取值范围.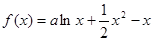
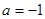 时,求函数
时,求函数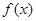 的单调区间;
的单调区间;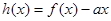 ,对定义域内任意x,均有
,对定义域内任意x,均有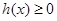 恒成立,求实数a的取值范围?
恒成立,求实数a的取值范围?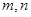 ,
,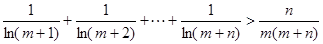 恒成立。
恒成立。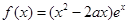 的图象大致是( )
的图象大致是( )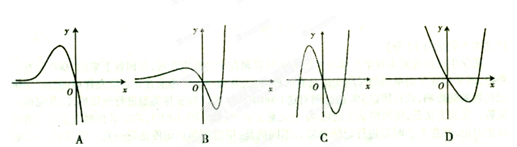
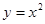 在
在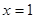 处的切线与两坐标轴围成三角形区域为
处的切线与两坐标轴围成三角形区域为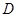 (包含三角形内部与边界).若点
(包含三角形内部与边界).若点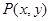 是区域
是区域 的取值范围是__________.
的取值范围是__________.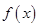 的导函数为
的导函数为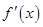 ,且满足关系式
,且满足关系式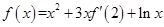 ,则
,则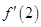 的值等于( )
的值等于( )

