题目内容
如图1,在平面内,ABCD是AB=2,BC=| 2 |
(1)求证:PE⊥平面ABCD;
(2)设二面角F-PB-D的平面角为θ,若θ≥45°,求线段CF长的取值范围.
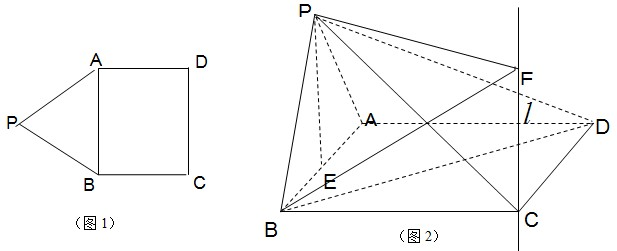
分析:(1)由题意得:BD⊥PE,PE⊥AB所以PE⊥平面ABCD.所以证明线面垂直一般是证明已知直线与平面内的两条相交直线垂直即可.
(2)建立空间直角坐标系利用向量法求出两个平面的法向量,结合向量的一个知识表示出向量的夹角,进而表示出二面角的平面角再求出线段CF长的取值范围.
(2)建立空间直角坐标系利用向量法求出两个平面的法向量,结合向量的一个知识表示出向量的夹角,进而表示出二面角的平面角再求出线段CF长的取值范围.
解答:解: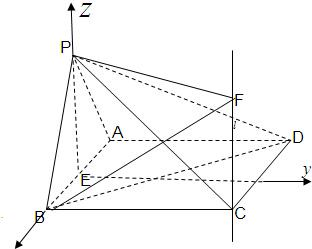 (1)连接EC,∵
(1)连接EC,∵
=
=
=
,∠EBC=∠BCD=90°,
∴△EBC∽△BCD,∴∠ECB=∠BDC.∴BD⊥CE.
又∵PC⊥BD,PC∩CE=C,∴BD⊥平面PEC.∴BD⊥PE.
在正△PAB中,∵E是AB的中点,∴PE⊥AB.
又∵AB∩BD=B,∴PE⊥平面ABCD.
(2))设CF=t.建立空间直角坐标系,如图,
则P(0,0,
),B(1,0,0),D(-1,
,0),F(1,
,t).
=(-2,
,0),
=(-1,0,
).
=(0,
,t).
设平面PBD的一个法向量为
=(x1,y1,1),
则
?
?
∴
=(
,
,1).
设平面FPB的一个法向量为
=(x2,y2,1),
则
?
?
∴
=(
,-
,1).
cosθ=|cos<
,
>|=
=
.
∵30°≤θ<45°,∴
≤sinθ<
.∴0<t≤
.
∵θ≥45°,∴cosθ≤
.
∴
≤
,化简得
t2-8
t-4≤0.
解得0<t≤8
+10
,因此,0<CF≤8
+10
.
 (1)连接EC,∵
(1)连接EC,∵| BE |
| BC |
| 1 | ||
|
| ||
| 2 |
| BC |
| CD |
∴△EBC∽△BCD,∴∠ECB=∠BDC.∴BD⊥CE.
又∵PC⊥BD,PC∩CE=C,∴BD⊥平面PEC.∴BD⊥PE.
在正△PAB中,∵E是AB的中点,∴PE⊥AB.
又∵AB∩BD=B,∴PE⊥平面ABCD.
(2))设CF=t.建立空间直角坐标系,如图,
则P(0,0,
| 3 |
| 2 |
| 2 |
| BD |
| 2 |
| BP |
| 3 |
| BF |
| 2 |
设平面PBD的一个法向量为
| n1 |
则
|
|
|
∴
| n1 |
| 3 |
| 6 |
设平面FPB的一个法向量为
| n1 |
则
|
|
|
∴
| n2 |
| 3 |
| t | ||
|
cosθ=|cos<
| n1 |
| n2 |
|
| ||||
|
|
|4-
| ||||||
|
∵30°≤θ<45°,∴
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∵θ≥45°,∴cosθ≤
| ||
| 2 |
∴
|4-
| ||||||
|
| ||
| 2 |
| 1 |
| 2 |
| 3 |
解得0<t≤8
| 3 |
| 2 |
| 3 |
| 2 |
点评:解决探索性问题与求长度问题最好的方法就是向量法,将其转化为向量的基本运算,通过方程或不等式解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
己知在锐角ΔABC中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]()
(I )求角![]() 大小;
大小;
(II)当![]() 时,求
时,求![]() 的取值范围.
的取值范围.

20.如图1,在平面内,![]() 是
是![]() 的矩形,
的矩形,![]() 是正三角形,将
是正三角形,将![]() 沿
沿![]() 折起,使
折起,使![]() 如图2,
如图2,![]() 为
为![]() 的中点,设直线
的中点,设直线![]() 过点
过点![]() 且垂直于矩形
且垂直于矩形![]() 所在平面,点
所在平面,点![]() 是直线
是直线![]() 上的一个动点,且与点
上的一个动点,且与点![]() 位于平面
位于平面![]() 的同侧。
的同侧。
(1)求证:![]() 平面
平面![]() ;
;
(2)设二面角![]() 的平面角为
的平面角为![]() ,若
,若![]() ,求线段
,求线段![]() 长的取值范围。
长的取值范围。


21.已知A,B是椭圆![]() 的左,右顶点,
的左,右顶点,![]() ,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线
,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线![]() 于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
(1)求椭圆C的方程;
 (2)求三角形MNT的面积的最大值
(2)求三角形MNT的面积的最大值
22. 已知函数![]()
![]() ,
,
(Ⅰ)若![]() 在
在![]() 上存在最大值与最小值,且其最大值与最小值的和为
上存在最大值与最小值,且其最大值与最小值的和为![]() ,试求
,试求![]() 和
和![]() 的值。
的值。
(Ⅱ)若![]() 为奇函数:
为奇函数:
(1)是否存在实数![]() ,使得
,使得![]() 在
在![]() 为增函数,
为增函数,![]() 为减函数,若存在,求出
为减函数,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)如果当![]() 时,都有
时,都有![]() 恒成立,试求
恒成立,试求![]() 的取值范围.
的取值范围.
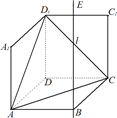 如图1,在平面内,ABCD是∠BAD=60°,且AB=a的菱形,ADD′′A1和CD D′C1都是正方形.将两个正方形分别沿AD,CD折起,使D′′与D′重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
如图1,在平面内,ABCD是∠BAD=60°,且AB=a的菱形,ADD′′A1和CD D′C1都是正方形.将两个正方形分别沿AD,CD折起,使D′′与D′重合于点D1.设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).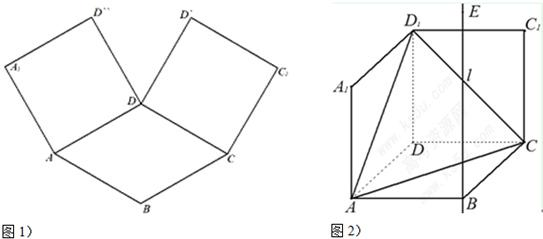
 的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).

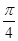 £ q £
£ q £  ,求线段BE长的取值范围;
,求线段BE长的取值范围; 上存在点
上存在点 ,使平面
,使平面 平面
平面 ,求
,求 与BE之间满足的关系式,并证明:当0 < BE < a时,恒有
与BE之间满足的关系式,并证明:当0 < BE < a时,恒有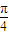 ≤θ≤
≤θ≤ ,求线段BE长的取值范围;
,求线段BE长的取值范围; 与BE之间满足的关系式,并证明:当0<BE<a时,恒有
与BE之间满足的关系式,并证明:当0<BE<a时,恒有 <1.
<1.