题目内容
4.已知等比数列{an}的公比为q,且数列{an+1}也是等比数列,试求q的值.分析 根据等比数列的定义进行证明即可.
解答 解:∵等比数列{an}的公比为q,
∴an=a1qn-1,
则an+1=1+a1qn-1,
若数列{an+1}也是等比数列,
则(a1+1)(a3+1)=(a2+1)2,
即(a1+1)(a1q2+1)=(qa1+1)2,
即a12q2+a1+a1q2+1=a12q2+2a1q+1
即1+q2=2q,即q2-2q+1=0,
则(q-1)2=0,
解得q=1.
点评 本题主要考查等比数列的判断,根据等比数列的定义和通项公式进行证明求解即可.

练习册系列答案
相关题目
12.如图所示的算法流程图运行后,输出结果是( )
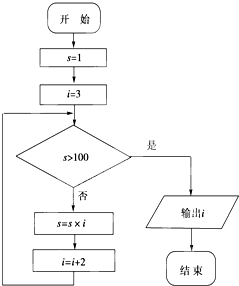

| A. | 7 | B. | 8 | C. | 9 | D. | 11 |
16.若平面α的一个法向量$\overrightarrow n$=(2,1,1),直线l的一个方向向量为$\overrightarrow a$=(1,2,3),则l与α所成角的正弦值为( )
| A. | $\frac{\sqrt{17}}{6}$ | B. | $\frac{\sqrt{21}}{6}$ | C. | -$\frac{\sqrt{21}}{6}$ | D. | $\frac{\sqrt{21}}{3}$ |
13.设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)•g(x)+f(x)•g′(x)>0,且f(-3)•g(-3)=0,则不等式f(x)•g(x)<0的解集是( )
| A. | (-3,0)∪(3,+∞) | B. | (-3,0)∪(0,3) | C. | (-∞,-3)∪(3,+∞) | D. | (-∞,-3)∪(0,3) |