题目内容
如图所示，在△ABC中，D，F分别是AB，AC的中点，BF与CD交于点O，设| AB |
| a |
| AC |
| b |
| a |
| b |
| AO |
分析：延长AO交BC于点E，利用重心定理及其向量的平行四边形法则可得：点E为BC的中点，
=
，
=
(
+
)，即可得出．
| AO |
| 2 |
| 3 |
| AE |
| AE |
| 1 |
| 2 |
| AB |
| AC |
解答：解：延长AO交BC于点E，则点E为BC的中点．
∴
=
，
=
(
+
)．
∴
=
×
×(
+
)=
+
．
∴
| AO |
| 2 |
| 3 |
| AE |
| AE |
| 1 |
| 2 |
| AB |
| AC |
∴
| AO |
| 2 |
| 3 |
| 1 |
| 2 |
| a |
| b |
| 1 |
| 3 |
| a |
| 1 |
| 3 |
| b |
点评：熟练掌握重心定理及其向量的平行四边形法则是解题的关键．
练习册系列答案
相关题目
如图所示，在△ABC，已知
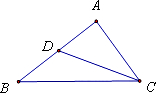如图所示，在△ABC中，点D是边AB的中点，则向量| DC |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
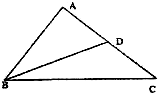如图所示，在△ABC中，∠B=60°，∠C=45°，高AD=
如图所示，在△ABC中，∠BAC=90°，∠ABC=60°，AD⊥BC于D，则
如图所示，在△ABC中，∠B=60°，∠C=45°，高AD=