题目内容
设函数f(x)=ax2-bx+1(a,b∈R),
(1)如果f(1)=0且对任意实数x均有f(x)≥0,求F(x)的解析式;
(2)在(1)在条件下,若g(x)=f(x)-kx在区间[-3,3]是单调函数,求实数k的取值范围;
(3)已知a>0且f(x)为偶函数,如果m+n>0,求证:F(m)+F(n)>0.
【答案】分析:(1)由f(1)=0,可得b=a+1,结合f(x)≥0恒成立,分a=0和a≠0两种情况讨论后可得a,b的值,进而求出函数f(x)的解析式,进而根据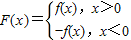 得到答案.
得到答案.
(2)若g(x)=f(x)-kx在区间[-3,3]是单调函数,函数区间[-3,3]在函数对称轴的同一侧,由此构造不等式可求出满足条件的实数k的取值范围;
(3)由f(x)为偶函数可得b=0,进而得到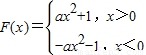 ,根据a>0,m+n>0,进而根据二次函数的图象和性质得到F(m)+F(n)的取值范围.
,根据a>0,m+n>0,进而根据二次函数的图象和性质得到F(m)+F(n)的取值范围.
解答:解(1)∵f(1)=0,
∴b=a+1(1分)
∵对任意实数x均有f(x)≥0恒成立,
即对任意实数x均有ax2-bx+1≥0恒成立(2分)
当a=0时,b=1,这时,f(x)=-x+1,它不满足f(x)≥0恒成立(3分)
当a≠0时,则a>0且△=(-b)2-4a=(a+1)2-4a=(a-1)2≤0
∴a=1,b=2(4分)
从而f(x)=x2-2x+1,
∴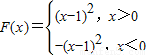 (5分)
(5分)
(2)由(1)知f(x)=x2-2x+1
∴g(x)=f(x)-kx=x2-(2+k)x+1=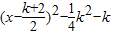 (6分)
(6分)
∵g(x)=f(x)-kx在区间[-3,3]是单调函数
∴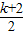 ≤3或
≤3或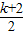 ≥3,
≥3,
即k≤-8或k≥4
∴k的取值范围是(-∞,-8]∪[4,+∞)(7分)
(3)∵f(x)是偶函数,
∴b=0(8分)
故f(x)=ax2+1,
∴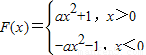 (9分)
(9分)
∵a>0,
∴当x>0时f(x)>0
∵m+n>0,
∴m,n中至少有一个正数,即m,n都是正数或一个正数,一个负数
若m,n都是正数,则F(m)>0,F(n)>0,所以F(m)+F(n)>0(10分)
若m,n一个正数,一个负数,不妨设m>,n<0,又m+n>0
则F(m)+F(n)=am2+1-(an2+1)=a(m+n)(m-n)>0(11分)
综上可得,F(m)+F(n)>0.(12分)
点评:本题考查的知识点是二次函数解析式的求法,二次函数的单调性,二次函数的图象,熟练掌握二次函数的图象和性质是解答的关键.
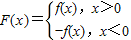 得到答案.
得到答案.(2)若g(x)=f(x)-kx在区间[-3,3]是单调函数,函数区间[-3,3]在函数对称轴的同一侧,由此构造不等式可求出满足条件的实数k的取值范围;
(3)由f(x)为偶函数可得b=0,进而得到
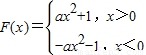 ,根据a>0,m+n>0,进而根据二次函数的图象和性质得到F(m)+F(n)的取值范围.
,根据a>0,m+n>0,进而根据二次函数的图象和性质得到F(m)+F(n)的取值范围.解答:解(1)∵f(1)=0,
∴b=a+1(1分)
∵对任意实数x均有f(x)≥0恒成立,
即对任意实数x均有ax2-bx+1≥0恒成立(2分)
当a=0时,b=1,这时,f(x)=-x+1,它不满足f(x)≥0恒成立(3分)
当a≠0时,则a>0且△=(-b)2-4a=(a+1)2-4a=(a-1)2≤0
∴a=1,b=2(4分)
从而f(x)=x2-2x+1,
∴
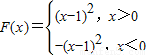 (5分)
(5分)(2)由(1)知f(x)=x2-2x+1
∴g(x)=f(x)-kx=x2-(2+k)x+1=
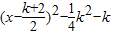 (6分)
(6分)∵g(x)=f(x)-kx在区间[-3,3]是单调函数
∴
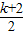 ≤3或
≤3或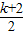 ≥3,
≥3,即k≤-8或k≥4
∴k的取值范围是(-∞,-8]∪[4,+∞)(7分)
(3)∵f(x)是偶函数,
∴b=0(8分)
故f(x)=ax2+1,
∴
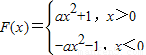 (9分)
(9分)∵a>0,
∴当x>0时f(x)>0
∵m+n>0,
∴m,n中至少有一个正数,即m,n都是正数或一个正数,一个负数
若m,n都是正数,则F(m)>0,F(n)>0,所以F(m)+F(n)>0(10分)
若m,n一个正数,一个负数,不妨设m>,n<0,又m+n>0
则F(m)+F(n)=am2+1-(an2+1)=a(m+n)(m-n)>0(11分)
综上可得,F(m)+F(n)>0.(12分)
点评:本题考查的知识点是二次函数解析式的求法,二次函数的单调性,二次函数的图象,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 设函数f(x)=(a
设函数f(x)=(a| x |
| 1 | ||
|
| ∫ | 2π π |
A、-
| ||
| B、-160 | ||
| C、160 | ||
| D、20 |